画像を微分するだけではどうしても微分値が小さいエッジが出てきてしまい、二値化した際に 途切れてしまう問題が発生する。これを解決するために、微分プラスαの検出方法を探索する。
目次
アルゴリズムの概要
非極大抑制
画像の微分値が極大となる画素のみをエッジの成分と見ることで、輪郭を太さ1ピクセルの線 として取得できるため、二重輪郭等のノイズを消せる可能性がある。
ヒステリシス処理
2つの閾値(低輝度側と高輝度側)を設定し、二つの閾値の中間に画像の微分値が来た時、微 分値が高輝度側の閾値を超えているピクセルと隣接している場合はエッジとみなす処理を行う ことで、途切れた輪郭を紡いでいくことが可能であると考えられる。また、これにより途切れ た輪郭を補完することができそうである。
ソーベルオペレータ
平滑化処理と水平、垂直方向微分を同時に行えるカーネルが存在するようである。
このカーネルを2方向の画像の微分値を得た後、勾配強度およびarctan(Gj/Gi)によりエッジの 勾配を求めることで非極大抑制アルゴリズムに落とし込めそうである。(8方向に場合分けして 考える必要がありそう。)
上記の処理をpython +OpenCV(Open Computer Vision)モジュールを用いて実装した。
実装手順
1.ソーベルオペレータの用意
平滑化と微分を同時に行うことができるソーベルオペレータを縦方向、横方向の2つに分けて 用意した。
kernel_i_sobel= np.array([[-1, 0, 1],[-2, 0, 2],[-1, 0, 1]])
kernel_j_sobel= np.array([[-1, -2, -1],[0, 0, 0],[1, 2, 1]])2.画像の微分
空間フィルタリング関数を作成し、横方向(Gx)、縦方向(Gj)にそれぞれに畳み込み演算結果を代入した。
def filter2d(img,kernel):
h,w = img.shape[0],img.shape[1]
dst = np.zeros((h,w))
d = int((kernel.shape[0]-1)/2)
for i in range(d,h-d):
for j in range(d,w-d):
dst[i][j] = np.sum(img[i-1:i+2,j-1:j+2]*kernel)
return dst
Gi = filter2d(img=img,kernel=kernel_i_sobel)
Gj = filter2d(img=img,kernel=kernel_j_sobel)上記の2つから勾配の強度Gと方向Gdを求めた。
G = np.sqrt(Gi**2 + Gj**2)
Gd = np.arctan2(Gj, Gi)ここで、画像データはピクセルが等間隔に並んでいることを考えると、注目画素に対し て 4 種類の勾配があることになるため、”平等”に角度を分割してピクセルの勾配を 4 方向に近似した。
def approx_gradient(G,Gd):
Gd = Gd
PI = np.pi
Gd[np.where((-1/8)*PI<=Gd<(1/8)*PI)] = 0
Gd[np.where((7/8)*PI<=Gd<PI)] = 0
Gd[np.where(-PI<=Gd<-(7/8)*PI)] = 0
Gd[np.where((1/8)*PI<=Gd<(3/8)*PI)] = PI/4
Gd[np.where(-(7/8)*PI<=Gd<-(5/8)*PI)] = PI/4
Gd[np.where((3/8)*PI<=Gd<(5/8)*PI)] = PI/2
Gd[np.where(-(5/8)*PI<=Gd<-(3/8)*PI)] = PI/2
Gd[np.where((5/8)*PI<=Gd<(7/8)*PI)] = 3*PI/4
Gd[np.where(-(3/8)*PI<=Gd<-(1/8)*PI)] = 3*PI/4
return Gd非極大抑制の実装
勾配方向を4方向に近似したことによって、注目画素の輝度が勾配方向の中で最大であ るかどうかの判定ができるようになった。これにより非極大抑制を行うことができる。
$$\begin{equation} \label{eq: cases f} f(i,j)= \begin{cases} f(i,j)& \text{$f(i,j)$が最大} \\ 0 & \text{それ以外} \end{cases} \end{equation}$$
上記の場合分けを用いて、以下のように関数approx_gradient()の返り値を引数として、非極大抑制処理を行う関数を作成した。
def NMS(G,Gd):
PI = np.pi
h= G.shape[1]
w = G.shape[0]
dst = G.copy()
for i in tqdm(range(1,w-1)):
for j in range(1,h-1):
target = Gd[i][j]
f = G[i][j]
if target== 0:
if max(G[i+1][j],f,G[i-1][j]) != f:
dst[i][j] = 0
else: pass
elif target == PI/4:
if max(G[i+1][j-1],f,G[i-1][j+1]) != f:
dst[i][j] = 0
else:
pass
elif target == PI/2:
if max(G[i][j-1],f,G[i][j+1]) != f:
dst[i][j] = 0
else:
pass
elif target == 3*PI/4:
if max(G[i-1][j-1],f,G[i+1][j+1]) != f:
dst[i][j] = 0
else:
pass
return dstヒステリシス処理の実装
下側の閾値l_thおよび上側の閾値h_thを指定し、以下の3パターンを考える。
$(1)\quad\text{$f(i,j)<l_{th}\quad (0\leq \exists l_{th}< h_{th})$}$
注目画素に最小輝度を代入。
$(2)\quad\text{$f(i,j)>h_{th}\quad (0\leq \exists l_{th}< h_{th})$}$
注目画素に最大輝度を代入。
$(3)\quad\text{$l_{th}<f(i,j)<h_{th}\quad (0\leq \exists l_{th}< h_{th})$}$
もし、周辺8近傍に、h_thを超えているものが一つでもあれば、信頼性が高いとみなし最大輝度を代入、そうでない場合は最小輝度を代入。
これらの条件を満たすように以下のようなアルゴリズムを作成した。
def hysteresis(img,l_th,h_th):
h,w = img.shape[1],img.shape[0]
dst = img.copy()
for i in tqdm(range(0,w)):
for j in range(0,h):
target = img[i][j]
dst_ij = dst[i][j]
if target < l_th:
dst_ij = 0
elif target >= h_th:
dst_ij = 255
else:
if np.max(img[i-1:i+2,j-1:j+2]) >= h_th:
dst_ij = 255
else:
dst_ij = 0
return dst以下に出力結果を示す。
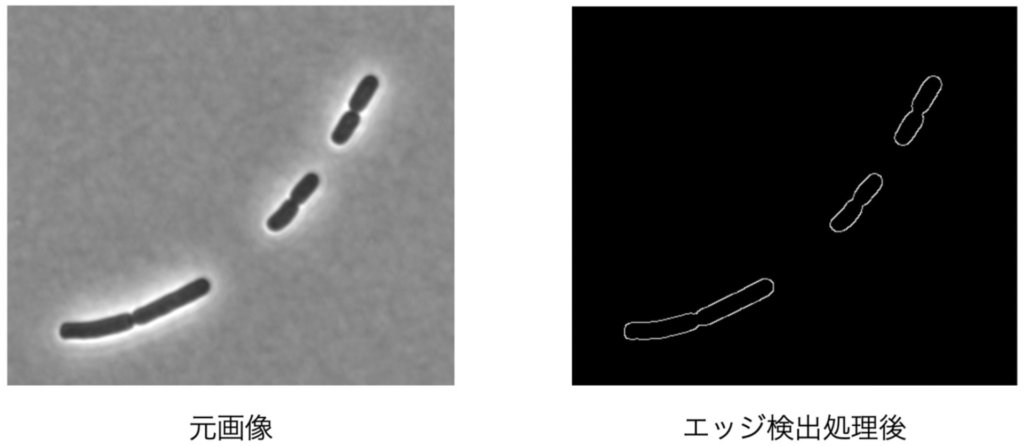
今後はこのエッジを経時的にトラッキングしていき、細胞増殖検出まで行えるようなアルゴリズムを構築する予定である。
参考文献:
https://ieeexplore.ieee.org/document/4767851



