高速フーリエ変換による空間周波数フィルタリング

画像解析でたまにフーリエ変換を使用するので、あらためてその詳細に迫ってみようと思います。

さらに、フーリエ逆変換を利用して任意の周波数領域のみを通過させる処理を行い、画像中のノイズ削除等を実装していきます。

フーリエ変換の復習

大学１年生くらいの時に、突然授業に出てきてさっぱり分かりませんでした。

よほどの数学好きではない限り、その意義を明確にしてもらわないと興味すら湧かないと思いますが、今は画像の信号解析という明確な目標があるためフーリエ変換の良いところを理解する気になりました。

連続関数に対するフーリエ変換(FT)

任意の実数ξにおいて、連続関数f(t)に対するフーリエ変換は以下のように表すことができます。

$$\displaystyle　\hat{f(\xi)}= \int^{\infty}_{-\infty} f(t) e^{-2\pi i t \xi } dt$$

この式によって、tの関数を角周波数の関数に変換することができます。

離散データに対する一次元フーリエ変換(DFT)

画像データはピクセルで区切られた離散的なデータであるため、上記の連続関数に対するフーリエ変換の式を使うことができません。

そのため、別途離散データに対するフーリエ変換を定義します。

$${\displaystyle F(k)=\sum _{x=0}^{N-1}f(x)\exp \left(-i{\frac {2\pi kx}{N}}\right)}$$

$W^{kx}_N$を回転子とすると

$$W^{kx}_N=\exp \left(-i{\frac {2\pi kx}{N}}\right)$$

であり、一次元離散フーリエ変換は

$${\displaystyle F(k)=\sum _{x=0}^{N-1}f(x)W^{kx}_N}$$

と表すことができます。

二次元フーリエ変換への拡張

上記の離散フーリエ変換は一次元に対するものですが、画像データは二次元配列なので離散フーリエ変換を二次元まで拡張します。

グレースケール画像をx列y行である明度関数f(x,y)とすると、

二次元離散フーリエ変換は

$${\displaystyle F(u,v)=\sum _{x=0}^{M-1} \sum _{y=0}^{N-1}f(x,y) e^{-2\pi i(\frac{ux}{M}+\frac{vy}{N})}}$$

となります。

少し変形すると

F(u,v)=\sum _{{x=0}}^{{M-1}}\left[\sum _{{y=0}}^{{N-1}}f(x,y)e^{{-2\pi i{\frac {vy}{N}}}}\right]e^{{-2\pi i{\frac {ux}{M}}}}

となり、この数式から、二次元フーリエ変換は一次元フーリエ変換を行と列それぞれに行ったものとみなすことができます。

つまり、二次元とは言えど一次元フーリエ変換を２方向に行えば良いということになります。

高速フーリエ変換(FFT)

上記の二次元フーリエ変換を行う際、サンプル数Nに対して時間計算量はO(N^2)となります。

ここで、離散的一次元フーリエ変換（DFT)をある関数に行列(W)処理を施すという見方をしてみると、

$$F=Wf$$

と表すことができます。

N=4の時

$N=2^2=4$において、周期性を利用すると

$(i) k=0,2$（偶数）の時

回転子$W^{kn}_4$は１またはその逆符号のみを取ります。

$(i) k=1,3$（奇数）の時

転子$W^{kn}_4$は$e^{-i\frac{6\pi}{4}}$、$e^{-i\frac{2\pi}{4}}$、$e^{-i\frac{18\pi}{4}}$の３パターンのみを取りますが、複素平面上の対称性を利用すると

$$W^{kn}_4=W^{1}_4,-W^{1}_4$$

の符号を考慮した一種類の値だけになります。

このことから、離散的一次元フーリエ変換をそのまま行なった時は16回の乗算を行う必要があるのに対して、高速フーリエ変換では１回のみの乗算で同じ計算結果を得ることができています。

計算量の削減

この時、計算量は$N^2$→$\frac {N}{2}(logN-1)$となっています。

つまり、時間計算量はO(NlogN)まで落とすことができたと言えます。

グラフにしてみると大きな違いがあることがわかります。

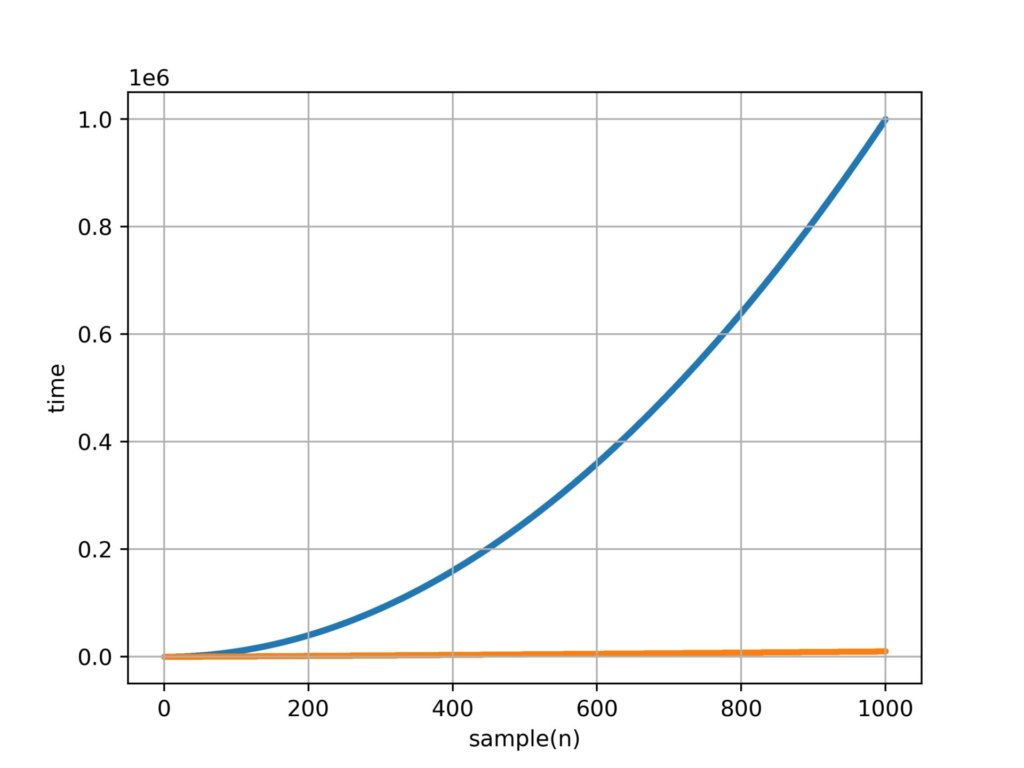
上記の理論を利用して高速フーリエ変換を行う際、対称性を利用するためNは２の冪乗になる必要がありますが、その場合に限りかなり計算量を落とすことができます。

高速フーリエ変換の実装

上記の理論をもとに、pythonで画像に対する高速フーリエ変換を実装していきます。

いつものようにwikipediaから酵母の顕微鏡写真を借りてきます。

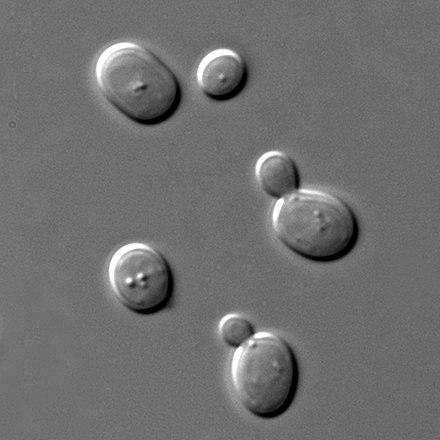
https://en.wikipedia.org/wiki/Saccharomyces_cerevisiae

numpy.fftメソッド

numpyモジュールに二次元高速フーリエ変換を行ってくれるメソッドがあるのでそれを使います。

from matplotlib import pyplot as plt
import cv2 
import numpy as np 
def get_fft_img(img,output_name):
    fig = plt.figure()
    img = cv2.imread(img,0)
    f = np.fft.fft2(img)
    fshift = np.fft.fftshift(f)
    magnitude_spectrum = 20*np.log(np.abs(fshift))
    plt.subplot(121),plt.imshow(img, cmap = 'gray')
    plt.title('Input Image'), plt.xticks([]), plt.yticks([])
    plt.subplot(122),plt.imshow(magnitude_spectrum, cmap = 'gray')
    plt.title('Magnitude Spectrum'), plt.xticks([]), plt.yticks([])
    fig.savefig(str(output_name)+'.jpg')
if __name__ =='__main__':
    get_fft_img('sample_1.jpg','a')

上記の処理で、画像を空間周波数領域に変換できました。

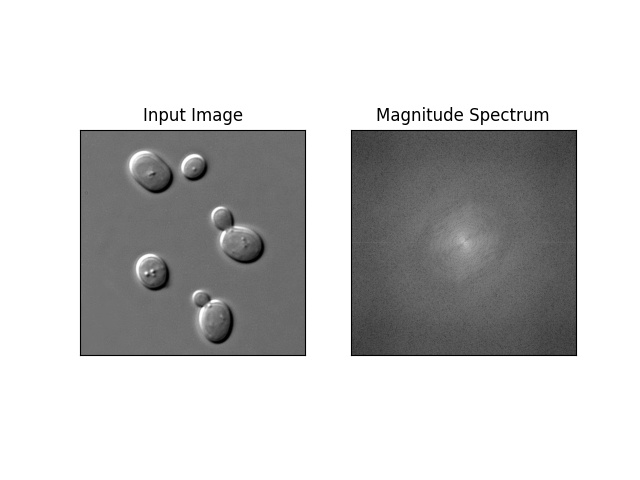
ローパスフィルタ

ローパスフィルタは、空間周波数領域の低周波成分のみを通過させたデータを逆フーリエ変換することでノイズを低減した画像を取得することができます。

以下実装例です。

import sys,cv2
import numpy as np
img = cv2.imread("sample_1.jpg",cv2.IMREAD_COLOR)
height, width, channels = img.shape[:3]
img = cv2.resize(img,(int(512),(int(512))))
img_gray = cv2.cvtColor(img,cv2.COLOR_RGB2GRAY)
img_fft = np.fft.fft2(img_gray)
img_fft = np.fft.fftshift(img_fft)
s = img_gray.shape
mask = np.zeros(s)
l= s[0]
c = s[0]/2
R = 15
for i in range(0,l):
    for j in range(0,l):
        if (i- c)**2 +(j- c)**2 <R**2:
            mask[i,j]=1
img_fft_filtered = img_fft*mask
img_fft_filtered= np.fft.fftshift(img_fft_filtered) 
iffimage = np.fft.ifft2(img_fft_filtered).real
cv2.imwrite('result_fft.jpg',np.uint8(iffimage))

実行結果

ガウシアンブラーのようにぼかしがかかっています。

ハイパスフィルタ

ハイパスフィルタはローパスフィルタの残りの周波数成分と考えることで簡単に実装できそうです。

import sys,cv2
import numpy as np
img = cv2.imread("sample_1.jpg",cv2.IMREAD_COLOR)
height, width, channels = img.shape[:3]
img = cv2.resize(img,(int(512),(int(512))))
img_gray = cv2.cvtColor(img,cv2.COLOR_RGB2GRAY)
img_fft = np.fft.fft2(img_gray)
img_fft = np.fft.fftshift(img_fft)
s = img_gray.shape
mask = np.zeros(s)
l= s[0]
c = s[0]/2
R = 30
for i in range(0,l):
    for j in range(0,l):
        if (i- c)**2 +(j- c)**2 >R**2:
            mask[i,j]=1
img_fft_filtered = img_fft*mask
img_fft_filtered= np.fft.fftshift(img_fft_filtered) 
iffimage = np.fft.ifft2(img_fft_filtered).real
cv2.imwrite('result_fft.jpg',np.uint8(iffimage))

実行結果