今回はラプラシアンカーネルを利用して、二次微分フィルタをかけていきたいと思います。
目次
微分について
通常、連続関数において以下の定義を微分と呼んでいます。
$$\displaystyle \frac{df}{dx} = \lim_{h \to 0} \frac{f(x+h) – f(x)}{h}$$
しかし、画像の場合信号が離散的なためこの定義を当てはめることができません。
そのため、画像については隣接画素との輝度差を勾配としてみることで微分と表しています。
一次微分カーネルの計算
明度関数f(i,j)に対し、水平方向と垂直方向の微分は以下のようになります。
水平方向微分:横方向のエッジの検出
$$\displaystyle \frac{\partial }{\partial i}f(i,j) =f(i+1,j)-f(i,j)$$
$$K_s = \begin{bmatrix}0&0&0\\0&-1&1\\0&0&0 \\ \end{bmatrix}$$
垂直方向微分:縦方向のエッジの検出
$$\displaystyle \frac{\partial }{\partial j}f(i,j) =f(i,j+1)-f(i,j) $$
$$K_l = \begin{bmatrix}0&1&0\\0&-1&0\\0&0&0 \\ \end{bmatrix}$$
位置(i,j)での明度関数の勾配ベクトルは明度関数の変化率が最大となる方向、つまり2方向のベクトルの足し合わせであるから
$$\ f'(i,j) = \sqrt{(\frac{\partial }{\partial i}f)^2+(\frac{\partial }{\partial j}f)^2}$$
となります。
一次微分を用いたフィルター処理は以下にまとめています。
二次微分カーネルの計算
一次微分を元に、もう一度差分を取りそれぞれ2方向の二次微分を求めます。
水平方向
$$\displaystyle \frac{\partial^2 }{\partial i^2}f=f(i+1,j)+f(i-1,j)-2f(i,j)$$
垂直方向
$$\displaystyle \frac{\partial^2 }{\partial j^2}f=f(i,j+1)+f(i,j-1)-2f(i,j)$$
ラプラシアンは
$$\nabla^2f=\displaystyle \frac{\partial^2 }{\partial i^2}f+\displaystyle \frac{\partial^2 }{\partial j^2}f$$
であるから
$$\nabla^2f=f(i+1,j)+f(i,j+1)$$
$$+f(i-1,j)+f(i,j-1)-4(i,j)$$
この結果から、4近傍カーネルは
$$K_4 = \begin{bmatrix}0&1&0\\1&-4&1\\0&1&0 \\ \end{bmatrix}$$
と表せます。
あとはこれを使ってフィルター処理を実装していきます。
畳み込み演算による実装
一次微分フィルタの時と同じように、生成した4近傍カーネルを使用して畳み込み演算を行なっていきます。
今回も同様の酵母の画像を使用してエッジの検出を行なってみます。
https://en.wikipedia.org/wiki/Saccharomyces_cerevisiae
初めに、カーネルを生成します。
kernel = np.array([[0, 1, 0],
[1, -4, 1],
[0, 1, 0]])import cv2
import numpy as np
import matplotlib.pyplot as plt
def filter2d(src, kernel):
m, n = kernel.shape
h = src.shape[0]
w = src.shape[1]
dst = np.zeros((h, w))
for y in range(int((m-1)/2), h - int((m-1)/2)):
for x in range(int((m-1)/2), w - int((m-1)/2)):
dst[y][x] = np.sum(src[y-int((m-1)/2):y+int((m-1)/2)+1, x-int((m-1)/2):x+int((m-1)/2)+1]*kernel)
return dst
img_raw = cv2.imread('sample_1.jpg')
img_gray = cv2.cvtColor(img_raw,cv2.COLOR_RGB2GRAY)
dst = filter2d(img_gray, kernel)
cv2.imwrite('result_Laplacian.jpg',dst)
以下が実行結果です。

OpenCVのfilter2Dメソッドを使用する方法もあります。
dst = cv2.filter2D(img_gray, cv2.CV_64F, kernel)8近傍カーネル
8近傍のラプラシアンカーネルは
$$K_8 = \begin{bmatrix}1&1&1\\1&-8&1\\1&1&1 \\ \end{bmatrix}$$
と表せます。
kernel = np.array([[1, 1, 1],
[1, -8, 1],
[1, 1, 1]])上記のカーネルを使用してフィルター処理を行なってみます。
img_raw = cv2.imread('sample_1.jpg')
img_gray = cv2.cvtColor(img_raw,cv2.COLOR_RGB2GRAY)
dst = filter2d(img_gray, kernel)
cv2.imwrite('result_Laplacian.jpg',dst)出力結果です。
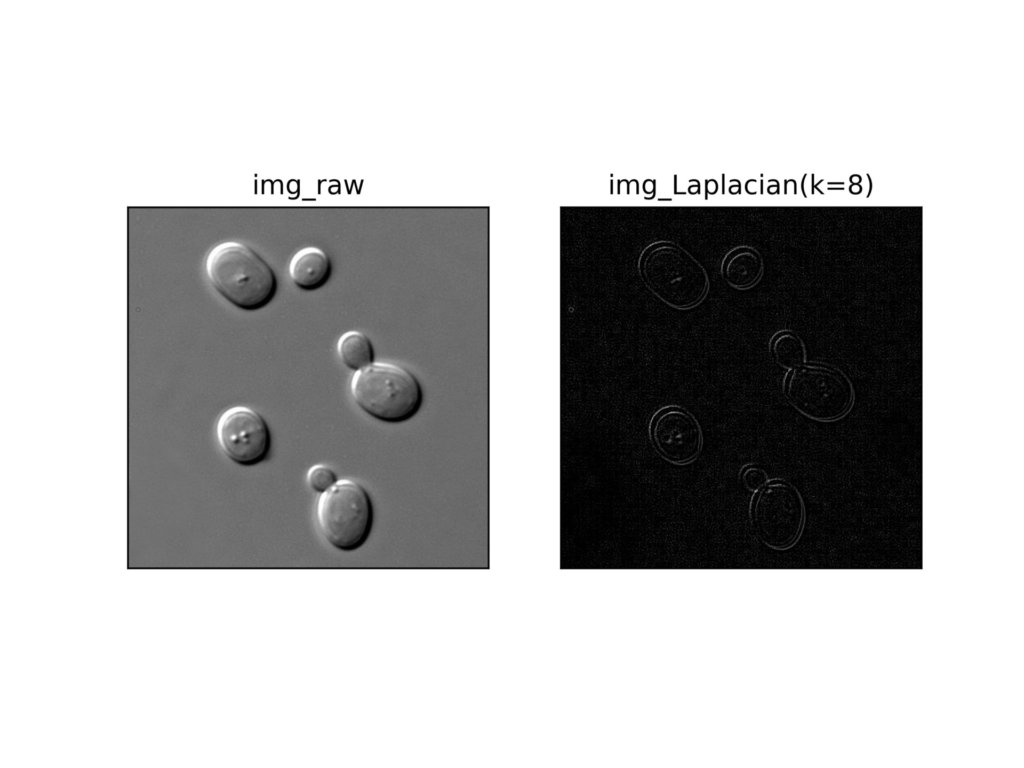
4近傍カーネルよりもはっきりとエッジ検出ができていますね。
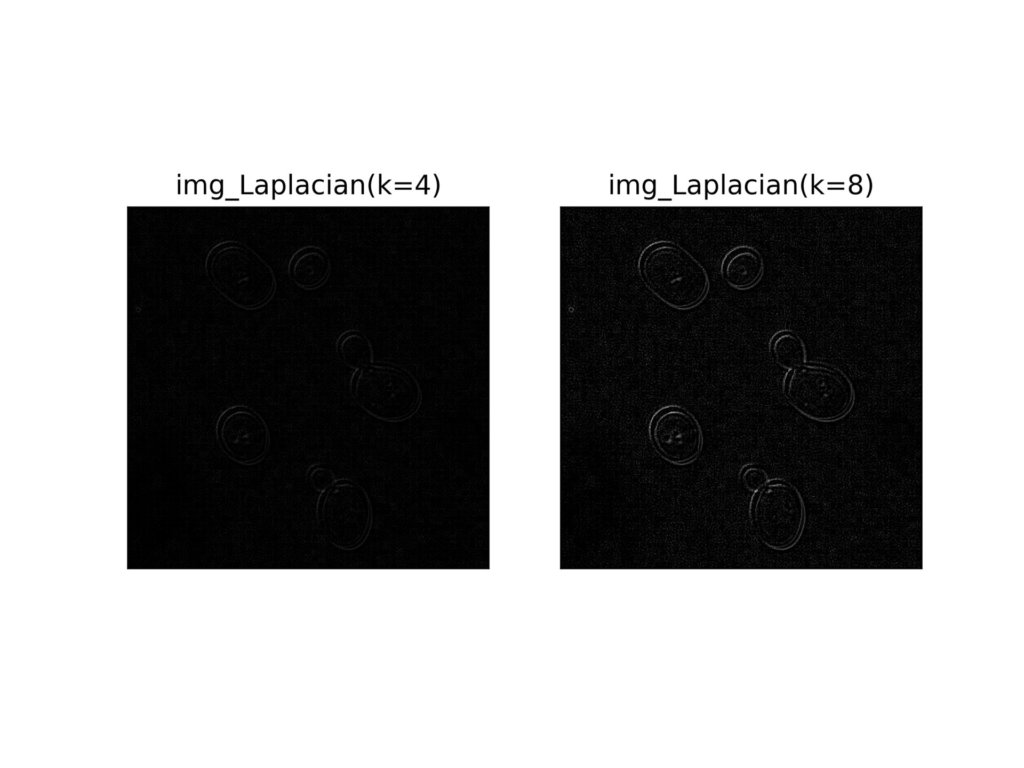
これは、8近傍カーネルが斜め4方向を考慮するためだと考えられます。
ksizeとノイズ
これは4近傍と8近傍カーネルの違いからもわかりますが、ksizeが上がるにつれいらない部分の輝度差(ノイズ)を強調してしまうというデメリットがあります。
この問題を解決するには、ガウシアンブラーを使用してノイズを低減してから処理を行う方法が考えられます。



