ミカエリスメンテン式

大学２年生で習ったミカエリスメンテン式を改めて復習します。

ミカエリスメンテン式

酵素反応はE(enzyme),S(substrate),P(product)を用いて以下のように表されます。

$$E+S\overset{k_{1}}{\underset{k_{-1}}{\rightleftharpoons}}ES\xrightarrow{k_2} P+E$$

ここで、Pの生成速度は

$$v_p=\frac{d[P]}{dt}=k_2[ES]\tag{1}$$

酵素基質複合体の生成速度は

$$\begin{align}v_{ES}&=\frac{d[ES]}{dt}\\&=k_1[E][S]-k_{-1}[ES]-k_2[ES]\quad (2)\end{align}$$

この時、以下の条件を満たす場合、酵素基質複合体は定常状態であると仮定できます。

条件1:酵素基質複合体の生成反応は平衡状態にある。

条件2:存在する全酵素は複合体を形成しており、基質濃度は酵素濃度よりも十分高い。

この時

$$\frac{d[ES]}{dt}=0\tag{3}$$

が成り立ちます。

(2)(3)式より

$$k_1[E][S]-k_{-1}[ES]-k_2[ES]=0\tag{4}$$

酵素の全濃度について

$$[E]_0 = [E]+[ES]\tag{5}$$

より、

$$\begin{align}[ES]&=\frac{[E]_0 [S]}{\frac{k_{-1}-k_2}{k_1}+[S]}\\&=\frac{[E]_0 [S]}{K_m+[S]}\tag{6}\end{align}$$

反応初期の微小時間中では基質と酵素が結合していないため、反応初速度を以下のようにすれば、

$$v=k_2[ES]$$

(6)式より

$$\begin{align}v&=\frac{k_2 [E]_0 [S]}{K_m + [S]}\\&=\frac{V_{max}[S]}{K_m+[S]}\tag{7}\end{align}$$

酵素の反応速度を得る。

Km値の意味

Km値はミカエリス定数と呼ばれます。

例えばKmが小さい場合、酵素の反応速度は大きくなります。つまり、基質との親和性が高いということができます。

Vmax

反応の最大速度であるVmaxは(7)式から

$$\lim_{[S] \to \infty}\frac{V_{max}[S]}{K_m+[S]}=V_{max}$$

となる。

Km=[S]のとき

(7)式について、Km=[S]となるとき、

$$v=\frac{V_{max}}{2}$$

となります。

Pythonで描画

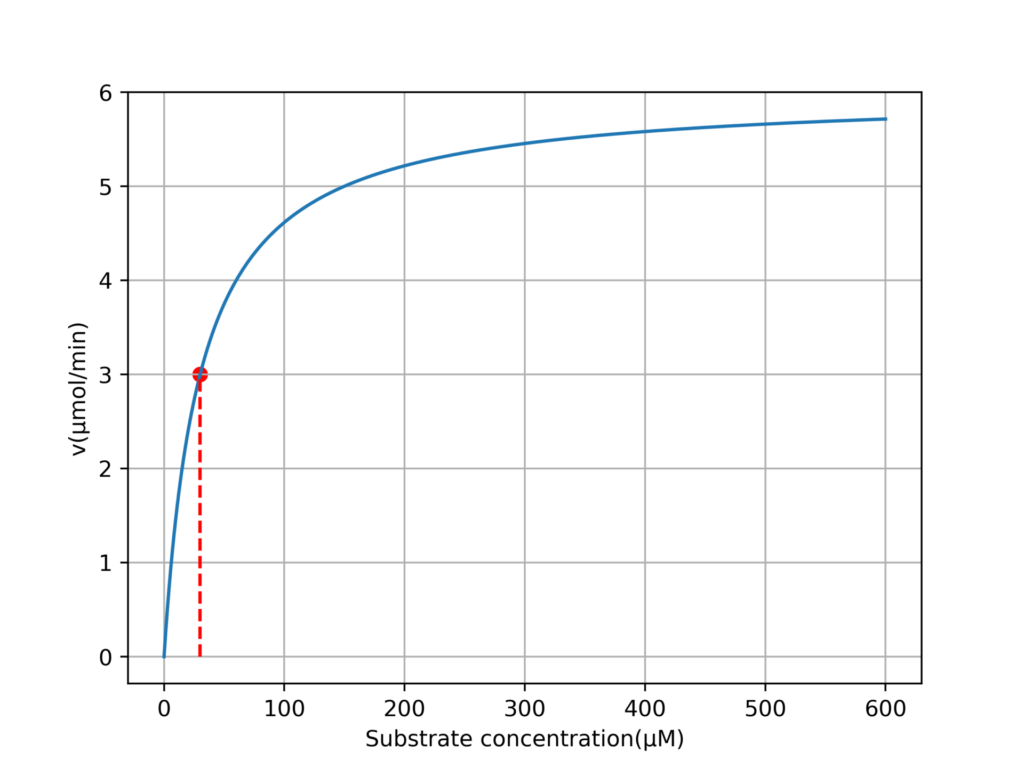
上記の式を踏まえて、具体的なグラフを作成してみます。（実際は計測データからKmとVmaxを求めることになりますが、これらのパラメータが決定していないとグラフ作成ができないため、今回は任意の値を指定します。）

Vmax=6(μmol/min),Km=30 (μM)の場合について考えます。

import numpy as np 
import matplotlib.pyplot as plt 

fig = plt.figure()
Km = 30
Vmax = 6
S = np.linspace(0,600,1000)
v = (Vmax*S/(Km+S))
plt.plot(S,v)
plt.grid()
plt.ylabel('v(μmol/min)')
plt.xlabel('Substrate concentration(μM)')
plt.vlines(Km,0, Vmax/2,color='red',linestyle = "dashed")
plt.scatter(Km,Vmax/2,color='red')

fig.savefig('result_mica.png',dpi=500)

出力結果