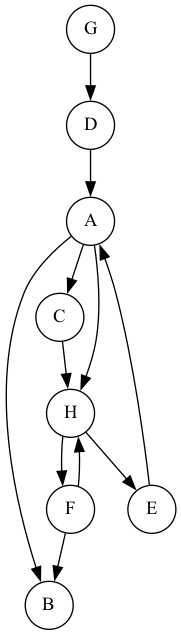
以下のようなグラフについて考えます。
import numpy as np
from graphviz import Digraph
G = Digraph(format="png",)
G.attr("node", shape="circle")
G.edge("A","B")
G.edge("A","C")
G.edge("A","H")
G.edge("C","H")
G.edge("H","F")
G.edge("H","E")
G.edge("E","A")
G.edge("F","B")
G.edge("F","H")
G.edge("G","D")
G.edge("D","A")
G = G.unflatten(stagger=2)
G.render("L.png")
目次
深さ優先探索(DFS)
Dをスタート地点とすると、探索毎のスタック構造は以下のようになります。
1 [D]
2 [D,A]
3 [D,A,B]
4 [D,A]
5 [D,A,C]
6 [D,A,C,H]
7 [D,A,C,H,E]
8 [D,A,C,H]
9 [D,A,C,H,F]
10 [D,A,C,H]
11 [D,A,C]
12 [D,A]
13 [D]
14 []
15 [G]
16 []
>>>
Discovery time, Finish time
D 1,14
A 2,13
B 3,14
C 5,12
H 6,11
E 7,8
F 9,10
G 15,16Pythonで実装
ノードクラスを作成してPythonで実装してみます。
class Node:
def __init__(self,name) -> None:
self.next_nodes:list[Node] = []
self.name:str = name
self.color: str = ""
self.prev:Node | None = None
self.finish_time:int = 0
self.discover_time:int = 0
pass
def set_next(self,data) -> None:
self.next_nodes.append(data)
def __repr__(self) -> str:
return f"{self.name}"
def set_color(self, color:str) -> None:
self.color = color
def get_color(self) -> str:
return self.color
def set_prev(self,prev) -> None:
self.prev = prev
def get_prev(self):
return self.prev
def set_finishtime(self,finish_time:int) -> None:
self.finish_time = finish_time
def set_discovertime(self,discover_time:int) -> None:
self.discover_time = discover_time
nodes = [Node(chr(i).upper()) for i in range(97,105)]
#A 0 B 1 C 2 D 3 E 4 F 5 G 6 H 7
nodes[6].set_next(nodes[3])
nodes[3].set_next(nodes[0])
nodes[0].set_next(nodes[1])
nodes[0].set_next(nodes[2])
nodes[0].set_next(nodes[7])
nodes[2].set_next(nodes[7])
nodes[7].set_next(nodes[4])
nodes[7].set_next(nodes[5])
nodes[4].set_next(nodes[0])
nodes[5].set_next(nodes[1])
nodes[5].set_next(nodes[7])
stack = [nodes[3]]
currNode:Node = stack[-1]
currNode.set_prev(None)
currNode.set_color("g")
currNode.set_discovertime(1)
i = 1
while len(stack) >0:
adj:list[Node]|list[None] = [i for i in currNode.next_nodes if i.get_color() != "g"]
print(i,f"{stack}")
if len(adj) == 0:
currNode = stack.pop(-1)
currNode.set_color("g")
currNode.set_finishtime(i+1)
if len(stack) == 0:
break
currNode = stack[-1]
else:
currNode = adj[0]
currNode.set_color("g")
stack.append(currNode)
currNode.set_discovertime(i+1)
i+=1
for i in nodes:
print(i.name,i.discover_time, i.finish_time)
>>>
1 [D]
2 [D, A]
3 [D, A, B]
4 [D, A]
5 [D, A, C]
6 [D, A, C, H]
7 [D, A, C, H, E]
8 [D, A, C, H]
9 [D, A, C, H, F]
10 [D, A, C, H]
11 [D, A, C]
12 [D, A]
13 [D]
#######
A 2 13
B 3 4
C 5 12
D 1 14
E 7 8
F 9 10
G 0 0
H 6 11幅優先探索
Dをスタート地点とすると、GはUnreachableとなります。
また、探索毎のキュー構造は以下のようになります。
1 [D]
2 [B,C,H]
3 [C,H]
4 [H]
5 [E,F]
6 [F]
7 []
Final depth
A 1
B 2
C 2
D 0
E 3
F 3
G -Pythonで実装
currNode:Node = nodes[3]
currNode.set_color("g")
currNode.set_discovertime(0)
queue = [i for i in currNode.next_nodes]
for i in queue:
i.set_color("g")
i.set_discovertime(1)
k = 2
while len(queue) > 0:
currNode = queue.pop(0)
print(currNode.next_nodes)
for i in currNode.next_nodes:
if i.discover_time > k:
i.set_discovertime(k)
if currNode.get_color() != "g":
currNode.set_color("g")
for i in [i for i in currNode.next_nodes if i.get_color() != "g" ]:
i.set_color("g")
queue += [j for j in i.next_nodes if j.get_color() != "g"]
k+=1
for i in nodes:
print(i.name,i.discover_time)
>>>
[B, C, H]
[E, F]
[A]
[B, H]
A 1
B 2
C 2
D 0
E 3
F 3
G inf
H 2


