サムネがコーヒーの記事は書きかけです。

Pythonでダイクストラ法の実装

SHARE

重み付きグラフにおいて、任意地点間の最短距離を求めるDijkstraアルゴリズムを実装してみます。

今回はGraphvizモジュールを使用して可視化しながら進めていきます。

アルゴリズム

一旦PseudoCodeの形で書きます。

グラフの生成

以下のような隣接行列を使用して、グラフを生成します。

$\mathbf{W}=\begin{pmatrix}0&0&0&0&0&0&0\\0&0&0&0&0&0&0\\3&0&0&0&0&0&0\\0&1&4&0&0&0&0\\0&2&1&0&0&3&0\\2&6&2&0&0&0&0\\0&2&0&0&0&5&0\end{pmatrix}$

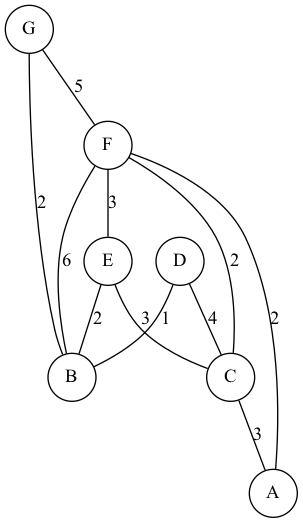
この時、Wは有向グラフであることに注意して、以下のように処理します。

$\mathbf{G} = \mathbf{W} + \mathbf{W}^{\mathrm{T}}$

よって、無向グラフGは

$\mathbf{G}=\begin{pmatrix}0&0&3&0&0&2&0\\0&0&0&1&2&6&2\\3&0&0&4&1&2&0\\0&1&4&0&0&0&0\\0&2&1&0&0&3&0\\2&6&2&0&3&0&5\\0&2&0&0&0&5&0\end{pmatrix}$

これをGraphvizで可視化すると、以下のようになります。

import matplotlib.pyplot as plt
import networkx as n 
import numpy as np 
from graphviz import Graph
G = np.array([
    #A  B  C  D  E  F  G
    [0, 0, 0, 0, 0, 0, 0], #A
    [0, 0, 0, 0, 0, 0, 0], #B
    [3, 0, 0, 0, 0, 0, 0], #C
    [0, 1, 4, 0, 0, 0, 0], #D
    [0, 2, 1, 0, 0, 3, 0], #E
    [2, 6, 2, 0, 0, 0, 0], #F
    [0, 2, 0, 0, 0, 5, 0]  #G
])

G += np.transpose(G)
G2 = Graph(format="png")
G2.attr("node", shape="circle")
nodes = [str(chr(i).upper()) for i in range(97,104)]
path_weights = {}
for i in range(len(G)):
    for j in range(len(G[0])):
        if G[i][j] != 0:
            G2.edge(str(nodes[i]),str(nodes[j]),label=str(G[i][j]))
            path_weights[f"{nodes[i]}->{nodes[j]}"] = G[i][j]
G2.render("AAAA")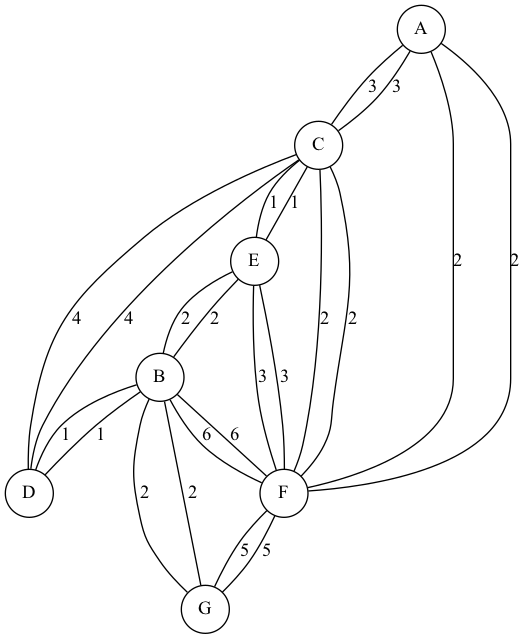

ノードの作成

ノードクラスを作成し、以下のような変数を定義します。

name -> ノード名

adj -> 隣接ノード

d -> estimate (無限遠に初期化）

explored -> 探索されたかどうかの真偽値

prevNode -> 直前のノード

class Node:
    def __init__(self,name:str) -> None:
        self.name:str = name
        self.adj:dict[str,int] = {}
        self.d:float = float('inf')
        self.explored:bool = False
        self.prevNode:Node | None = None
    
    def __repr__(self) -> str:
        return self.name

    def set_explored(self,e:bool) -> None:
        self.explored = e

    def set_d(self,d:int) -> None:
        self.d = d

探索アルゴリズムの実装とバックトラック

キューを利用した幅優先探索を行い、startNode, endNodeの二地点間の距離が最小となるパスを探します。探索終了後は、末尾ノードからバックトラックをして先端のノードまで辿っていきます。

class PathFinder:
    def __init__(self,all_paths:dict[str,int],nodes_string:list[str]) -> None:
        self.nodes_string: list[str] = nodes_string
        self.nodes:dict[str,Node] = {i:Node(i) for i in nodes_string}
        for i in all_paths.keys():
            self.nodes[i[0]].adj[i[3]] = all_paths[i]
    
    def dijkstra(self,startNode:str,endNode:str):

        #最短距離を無限大に初期化
        for i in self.nodes.keys():
            self.nodes[i].d = float('inf')

       
        queue:list[str] = [startNode]
        #currNodeを初期化
        currNode: str = queue[0]
        #currNodeの距離を初期化
        self.nodes[currNode].set_d(0)
        #初期ノードのprevNodeを初期化
        self.nodes[currNode].prevNode = None


        while len(queue) >0:
            currNode = queue.pop(0)
            adjs = self.nodes[currNode].adj
            for i in adjs.keys():
                tmp_d:float = self.nodes[currNode].d + self.nodes[currNode].adj[i]
                if self.nodes[i].d > tmp_d:
                    #スタートノードからの最短到達距離を更新
                    self.nodes[i].set_d(int(tmp_d))
                    self.nodes[i].prevNode = self.nodes[currNode]
                    self.nodes[i].set_explored(True)
                    queue.append(i)
        cNode:Node = self.nodes[endNode]
    
        #バックトラック
        s:list[str] = [endNode]
        while cNode.prevNode != None:
            cNode = cNode.prevNode
            s.append(cNode.name)

        return [s[::-1],self.nodes[endNode].d]




W = PathFinder(path_weights,nodes)

print(W.dijkstra("A","B"))
print(W.dijkstra("B","A"))
print(W.dijkstra("D","C"))
print(W.dijkstra("E","F"))
print(W.dijkstra("A","D"))

>>>
[['A', 'C', 'E', 'B'], 6]
[['B', 'E', 'C', 'A'], 6]
[['D', 'C'], 4]
[['E', 'F'], 3]
[['A', 'C', 'D'], 7]

NetworkXで検証

ダイクストラアルゴリズムを標準実装しているNetworkXと比べてみます。

まずはNetworkXで隣接行列からグラフを作成します。

import matplotlib.pyplot as plt
import networkx as n 
import numpy as np 

G = np.array([
    #A  B  C  D  E  F  G
    [0, 0, 0, 0, 0, 0, 0], #A
    [0, 0, 0, 0, 0, 0, 0], #B
    [3, 0, 0, 0, 0, 0, 0], #C
    [0, 1, 4, 0, 0, 0, 0], #D
    [0, 2, 1, 0, 0, 3, 0], #E
    [2, 6, 2, 0, 0, 0, 0], #F
    [0, 2, 0, 0, 0, 5, 0]  #G
])

G += np.transpose(G)
#GraphD class
class GraphD:
    def __init__(self) -> None:
        #networkx object
        self.G = n.DiGraph()
#GraphD object
graphD = GraphD()

nodes = [chr(i).upper() for i in range(97,104)]
graphD.G.add_nodes_from(nodes)
for i in range(len(G)):
    for j in range(len(G[0])):
        if G[i][j] != 0:
            graphD.G.add_weighted_edges_from([(nodes[i],nodes[j],G[i][j])])

pos = n.spring_layout(graphD.G)
fig = plt.figure()
n.draw_networkx_nodes(graphD.G, pos, node_size=300)
n.draw_networkx_edges(graphD.G, pos, width=2)
n.draw_networkx_labels(graphD.G, pos, font_size=10, font_color="black")
n.draw_networkx_edge_labels(graphD.G, pos, edge_labels={(i, j): w['weight'] for i, j, w in graphD.G.edges(data=True)})
fig.savefig("result1.png",dpi = 500)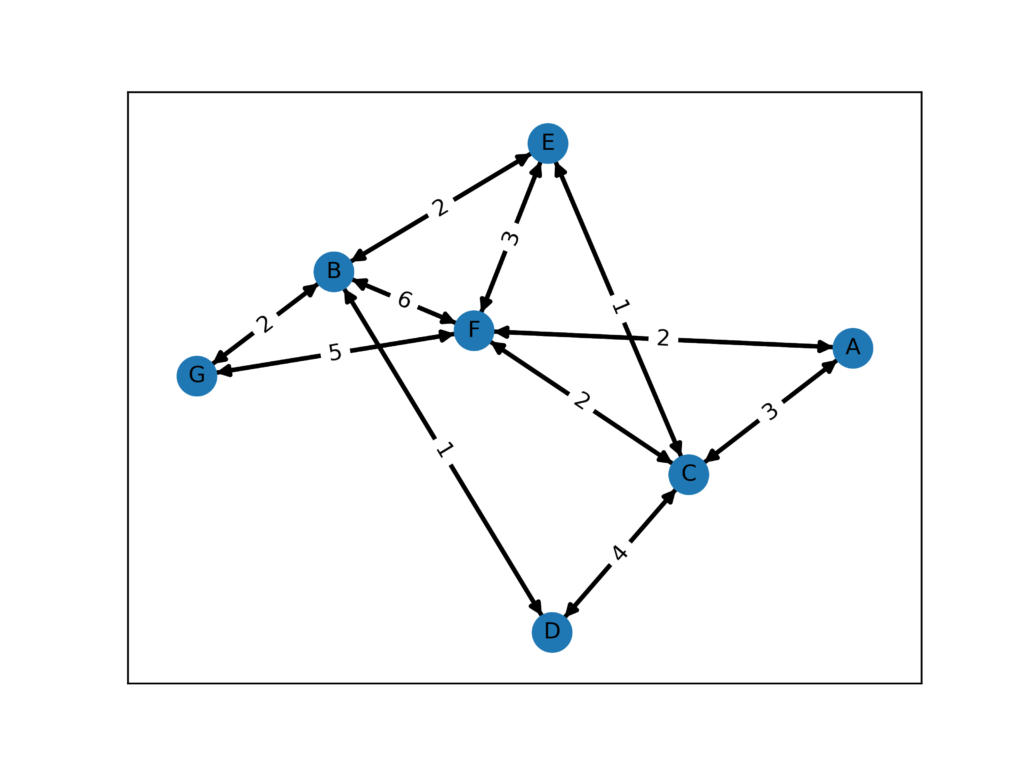

グラフ構造ができたので、自前で実装したアルゴリズムとnxビルトインのダイクストラアルゴリズムを使用して結果を検証します。

#検証
import networkx as n 
#GraphD class
class GraphD:
    def __init__(self) -> None:
        #networkx object
        self.G = n.DiGraph()

#GraphD object
graphD = GraphD()

nodes = [str(chr(i).upper()) for i in range(97,104)]
graphD.G.add_nodes_from(nodes)
for i in range(len(G)):
    for j in range(len(G[0])):
        if G[i][j] != 0:
            graphD.G.add_weighted_edges_from([(nodes[i],nodes[j],G[i][j])])

for i in range(len(G)):
    for j in range(len(G)):
        if i != j:
            W = PathFinder(path_weights,nodes)
            nx_dijkstra = [n.dijkstra_path(graphD.G, nodes[i], nodes[j]),n.dijkstra_path_length(graphD.G, nodes[i], nodes[j])]
            naive_dijkstra = [i for i in W.dijkstra( nodes[i], nodes[j])]
            if nx_dijkstra[1] != naive_dijkstra[1]:
                print(nx_dijkstra)
                print(naive_dijkstra)
                print("Test failed.")
>>>
None

ランダム経路の生成と探索

対角成分が０の隣接行列をランダムに生成後、全ノード間の最短距離を計算するプログラムを書いてみます。

import matplotlib.pyplot as plt
import networkx as n 
import numpy as np 
from graphviz import Graph
import random 

G = np.array([
    #A  B  C  D  E  F  G
    [0, 0, 0, 0, 0, 0, 0], #A
    [0, 0, 0, 0, 0, 0, 0], #B
    [3, 0, 0, 0, 0, 0, 0], #C
    [0, 1, 4, 0, 0, 0, 0], #D
    [0, 2, 1, 0, 0, 3, 0], #E
    [2, 6, 2, 0, 0, 0, 0], #F
    [0, 2, 0, 0, 0, 5, 0]  #G
])


k = 100

G =[[0 for i in range(k)] for j in range(k)]
rand_weigts = [0 for i in range(k)] + [random.randint(0,100) for i in range(10)]
for i in range(len(G)):
    for j in range(len(G)):
        if i<j:
            G[i][j] = random.choice(rand_weigts)

print(G)

G += np.transpose(G)

print(G)
G2 = Graph(format="png")
G2.attr("node", shape="circle")
nodes = [f"N{str(i)}" for i in range(k)]

path_weights = {}
for i in range(len(G)):
    for j in range(len(G[0])):
        if G[i][j] != 0:
            G2.edge(str(nodes[i]),str(nodes[j]),label=str(G[i][j]))
            path_weights[f"{nodes[i]}->{nodes[j]}"] = G[i][j]
# G2.render("AAAA")

class Node:
    def __init__(self,name:str) -> None:
        self.name:str = name
        self.adj:dict[str,int] = {}
        self.d:float = float('inf')
        self.explored:bool = False
        self.prevNode:Node | None = None
    
    def __repr__(self) -> str:
        return self.name

    def set_explored(self,e:bool) -> None:
        self.explored = e

    def set_d(self,d:int) -> None:
        self.d = d 

class PathFinder:
    def __init__(self,all_paths:dict[str,int],nodes_string:list[str]) -> None:
        self.nodes_string: list[str] = nodes_string
        self.nodes:dict[str,Node] = {i:Node(i) for i in nodes_string}
        for i in all_paths.keys():
            tmp = i.split("->")
            self.nodes[tmp[0]].adj[tmp[1]] = all_paths[i]
    
    def dijkstra(self,startNode:str,endNode:str):

        #最短距離を無限大に初期化
        for i in self.nodes.keys():
            self.nodes[i].d = float('inf')
        
        queue:list[str] = [startNode]
        #currNodeを初期化
        currNode: str = queue[0]
        #currNodeの距離を初期化
        self.nodes[currNode].set_d(0)
        #初期ノードのprevNodeを初期化
        self.nodes[currNode].prevNode = None


        while len(queue) >0:
            currNode = queue.pop(0) 
            
            adjs = self.nodes[currNode].adj
      
            for i in adjs.keys():
                tmp_d:float = self.nodes[currNode].d + self.nodes[currNode].adj[i]
                if self.nodes[i].d > tmp_d:
                    self.nodes[i].set_d(int(tmp_d))
                    self.nodes[i].prevNode = self.nodes[currNode]
                    self.nodes[i].set_explored(True)
                    queue.append(i)
        cNode:Node = self.nodes[endNode]
    
        #バックトラック
        s:list[str] = [endNode]
        while cNode.prevNode != None:
            cNode = cNode.prevNode
            s.append(cNode.name)

        return [s[::-1],self.nodes[endNode].d]
    
W = PathFinder(path_weights,nodes)


#検証
import networkx as n 
#GraphD class
class GraphD:
    def __init__(self) -> None:
        #networkx object
        self.G = n.DiGraph()
#GraphD object
graphD = GraphD()


graphD.G.add_nodes_from(nodes)
for i in range(len(G)):
    for j in range(len(G[0])):
        if G[i][j] != 0:
            graphD.G.add_weighted_edges_from([(nodes[i],nodes[j],G[i][j])])

for i in range(len(G)):
    for j in range(len(G)):
        if i != j:
            W = PathFinder(path_weights,nodes)
            nx_dijkstra = [n.dijkstra_path(graphD.G, nodes[i], nodes[j]),n.dijkstra_path_length(graphD.G, nodes[i], nodes[j])]
            naive_dijkstra = [i for i in W.dijkstra( nodes[i], nodes[j])]
            if nx_dijkstra[1] != naive_dijkstra[1]:
                #print(nx_dijkstra)
                print(naive_dijkstra)
                print("Test failed.")
            else:
                print(f"Pathfinder:{naive_dijkstra}")
                print(f"NetWorkX:{nx_dijkstra}")

コメントを残す

メールアドレスが公開されることはありません。 ※ が付いている欄は必須項目です

前の記事

有向グラフの幅優先探索と深さ優先探索【グラフ理論】

次の記事

JavaScriptまとめ