二分探索木の反転 Java

どこで使うかわかりませんが、二分探索木を水平方向に反転させるアルゴリズムを作ります。

例えば、以下のような二分探索木があったとします。

public class BinaryTree<T extends Comparable<T>> {


    private Node<T> root;
    
    public BinaryTree(Node<T> root) {
        this.root = root;
    }

    public Node<T> getRoot() {
        return this.root;
    }

    public void inorder(Node<T> node){
        if (node == null){
            return;
        }else{
            inorder(node.getLeft());
            
            System.out.print(node.getData()+" ");
            inorder(node.getRight());
        }
    }


    public static void main(String[] args) {

        BinaryTree<Integer> t1 = new BinaryTree<Integer>(new Node<>(2,new Node<>(1),new Node<>(null)));

        BinaryTree<Integer> t2 = new BinaryTree<Integer>(new Node<>(3,t1.root,new Node<>(4)));

        BinaryTree<Integer> t3 = new BinaryTree<Integer>(new Node<>(6,new Node<>(null),new Node<>(7)));

        BinaryTree<Integer> t4 = new BinaryTree<Integer>(new Node<>(8,t3.root,new Node<>(null)));

        BinaryTree<Integer> binaryTree = new BinaryTree<Integer>(new Node<>(5,t2.root,t4.root));
        
        System.out.println("Inorder:");
        binaryTree.inorder(binaryTree.getRoot());
        
    }
}

これを可視化すると、

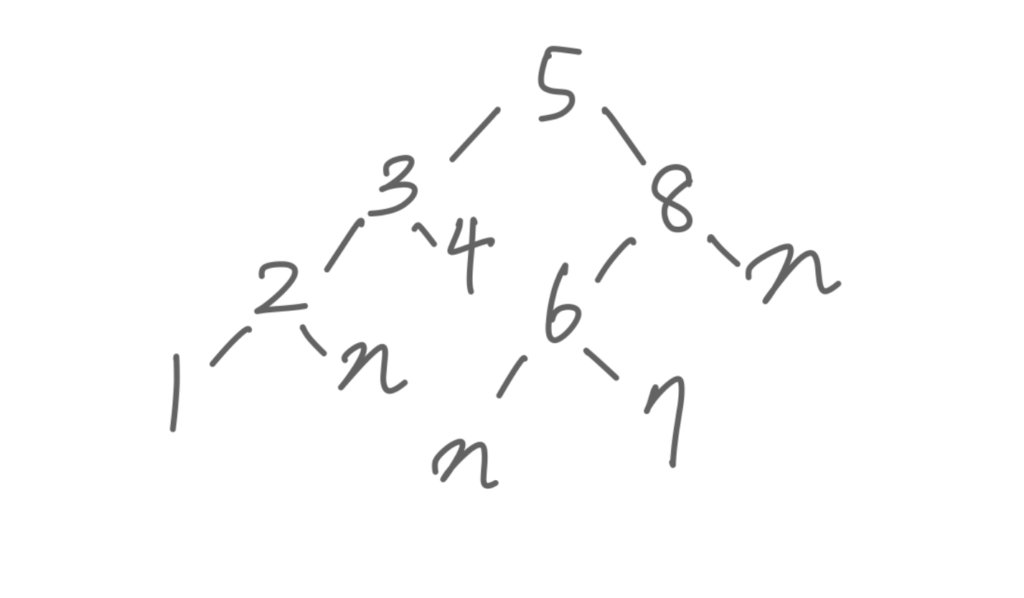
この図のようになります。

この二分探索木に対して、深さ優先で走査を行うと図のように順番に値を取得できることがわかります。

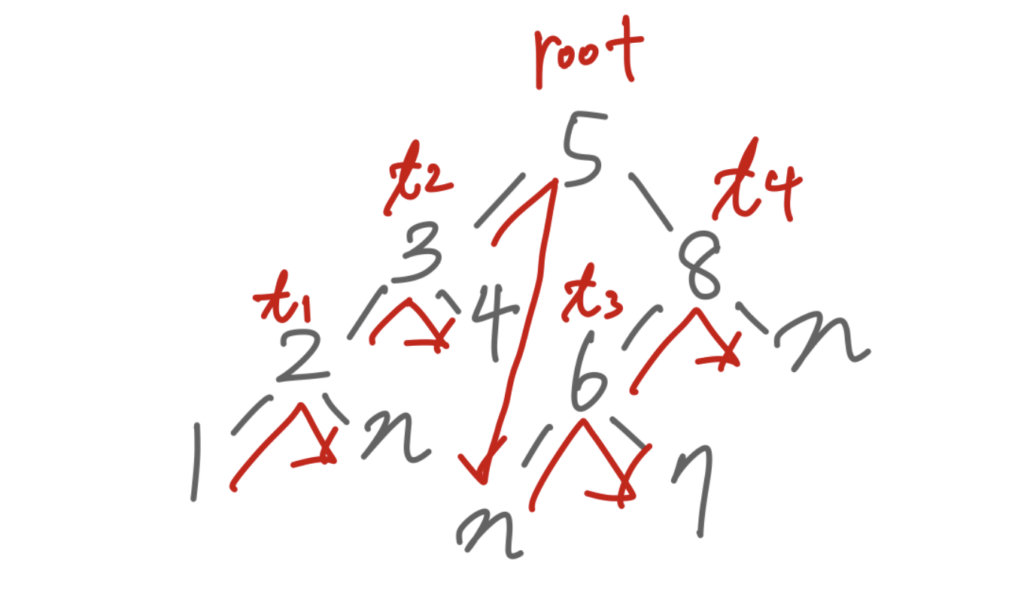
これをrootを軸として水平方向に反転するには、巡回アルゴリズムを少し変更して深い方のノードから要素の反転を繰り返せば良いことがわかります。

よって、

public Node<T> invert(Node<T> node) {
        if (node == null) {
            return node;
        }else{
            invert(node.getLeft());
            invert(node.getRight());
            Node<T> tmp = node.getLeft();
            node.setLeft(node.getRight()); 
            node.setRight(tmp);
            return node;
        }
    }

これを確認してみると、

public static void main(String[] args) {
        System.out.println("Inorder:");
        binaryTree.inorder(binaryTree.getRoot());
        binaryTree.invert(binaryTree.root);
        System.out.println();
        binaryTree.inorder(binaryTree.getRoot());
    }

>>>
Inorder:
1 2 null 3 4 5 null 6 7 8 null 
null 8 7 6 null 5 4 3 null 2 1 %

反転できていることがわかります。

今のところうまく可視化する手段を確立していないので、今後模索していきます。