対角化を行うには、固有値の計算と対角化可能かを知るための固有ベクトルの計算が必要になります。
目次
固有値、固有ベクトルの復習
n次正方行列について
$A\textbf{v}=\lambda\textbf{v}\{\lambda \in \mathbb{R} | \textbf{v}\in \mathbb{R}^n \}$を満たすλをAの固有値、この時のvをAの固有ベクトルと言います。
対角化可能か判別する
$A = \begin{pmatrix}a & b \\c & d \end{pmatrix}$
があるとすると、初めに
$det(\lambda I-A)=0$となるλを探します。
ここで見つかったλを用いて、対角行列Dは
$D = \begin{pmatrix}\lambda_1& 0\\ 0& \lambda_2\end{pmatrix}$
また、λの固有空間$W_{\lambda_i}=\{v_i\in\mathbb{C}^n|A\textbf{v}=\lambda\textbf{v}\}=Ker(A-\lambda I)$
は$(A-\lambda I)\textbf{v}=0$の解と一致するので、
固有ベクトル $\textbf{v} = t\begin{pmatrix}C_1\\C_2 \end{pmatrix} (\forall{t}\in\mathbb{R})$
上記から固有ベクトルの列ベクトルを$P= \begin{pmatrix}C_{11} & C_{12} \\ C_{21}& C_{22} \end{pmatrix}$とおきます。
この時、$P^{-1}AP=D$が成り立つならばAは対角化可能と言えます。
Pythonでの実装
2次元正方行列についてpythonで対角化を実装していきます。
import sympy as sp
l = sp.symbols('λ')
A = [[7,-6],[3,-2]]
det = (l**2)-(A[0][0]+A[1][1])*l-A[0][1]*A[1][0] + A[0][0]*A[1][1]
b = -(A[0][0]+A[1][1])
c = A[0][0]*A[1][1] - A[0][1]*A[1][0]
l1 = ((-b)+sp.sqrt(b**2-4*c))/2
l2 = ((-b)-sp.sqrt(b**2-4*c))/2
print(l1)
print(det)
D = [[l1,0],[0,l2]]
print(D)さて、対角化行列を取得するプログラムができましたが、そもそも対角化可能かを確かめることができません。そこで、モジュールの力を利用して実装していきます。
Numpyで実装
行列計算を高速に行えるnumpyを使用して実装していきます。
import numpy as np
def diag(A):
eigenvector, P = np.linalg.eig(A)
if len(set(eigenvector)) == len(A):
return np.dot(np.dot(np.linalg.inv(P), A), P)
else:
print("Unable to diagonalizate")
return None
A = np.array([[7, -6],
[3, -2]])
print(diag(A))numpyは対角化可能判定を行なってくれないため、n次元正方行列の固有値が次元数と一致していなければNonetypeとする処理を追加しています。
行列の冪乗計算
行列Aの固有ベクトルの列ベクトルPの逆行列を$P^{-1}$とすると、$P^{-1}AP=D$が成り立ちます。
これは$A=PDP^{-1}$と書き換えることができるます。ここで$P^{-1}P$が基底ベクトルを固有基底に基底変換しているだけであることを踏まえると、どれだけ冪乗処理を行っても$A^n=PD^nP^{-1}$となるはずです。この性質を利用すれば、行列の冪乗を高速化することができそうなので、実際にやってみます。
通常の冪乗
冪乗にはnp.dotメソッドを使用します。オーバーフローしないように要素は控えめにしています。
import time
t0 = time.clock_gettime_ns(time.CLOCK_MONOTONIC)
A = np.array([[1.001, 1.002],
[1.003, 1.004]])
n = 1000
A1 = A
for i in range(n-1):
A1 = np.dot(A1,A)
print(A1)
t1 = time.clock_gettime_ns(time.CLOCK_MONOTONIC)
print(t1-t0)実行結果
[[6.49999051e+301 6.50647753e+301]
[6.51297102e+301 6.51947098e+301]]
1389000対角化行列の冪乗
t0 = time.clock_gettime_ns(time.CLOCK_MONOTONIC)
A = np.array([[1.001, 1.002],
[1.003, 1.004]])
n = 1000
r = diag(A)
D = r[0]
P = r[1]
P_inv = np.linalg.inv(P)
A2 = np.dot(np.dot(P,D**n),P_inv)
t1 = time.clock_gettime_ns(time.CLOCK_MONOTONIC)
print(t1-t0)実行結果
[[6.49999051e+301 6.50647753e+301]
[6.51297102e+301 6.51947098e+301]]
2318000高速かと思ったら逆にクソ遅くなっていました。どこかで逆転させたいので次元を上げていきます。
n次元での対角化と通常の冪乗
n次元正方行列を生成していき、どこから対角化の威力が出てくるかを求めていきます。ちなみに、対角化の操作を最適化したnpメソッドも使用して3つの方法での対決です。
fig = plt.figure()
for i in range(2,40):
A = np.array([[1.00001+0.00001*k for j in range(i)] for k in range(i)])
n = 100
t0 = time.clock_gettime_ns(time.CLOCK_MONOTONIC)
D, P = np.linalg.eig(A)
P_inv = np.linalg.inv(P)
A2 = np.dot(np.dot(P,D**n),P_inv)
t1 = time.clock_gettime_ns(time.CLOCK_MONOTONIC)
plt.scatter(i,t1-t0,color = 'red',s=15)
t0 = time.clock_gettime_ns(time.CLOCK_MONOTONIC)
A1 = A
for k in range(i-1):
A1 = np.dot(A1,A)
t1 = time.clock_gettime_ns(time.CLOCK_MONOTONIC)
plt.scatter(i,t1-t0,color = 'blue',s=15)
t0 = time.clock_gettime_ns(time.CLOCK_MONOTONIC)
A3 = np.linalg.matrix_power(A, n)
t1 = time.clock_gettime_ns(time.CLOCK_MONOTONIC)
plt.scatter(i,t1-t0,color = 'green',s=15)
fig.savefig("s.png",dpi=500)
実行結果
青が通常の掛け算、緑が高速計算、赤が手動での対角化による冪乗の計算時間です。
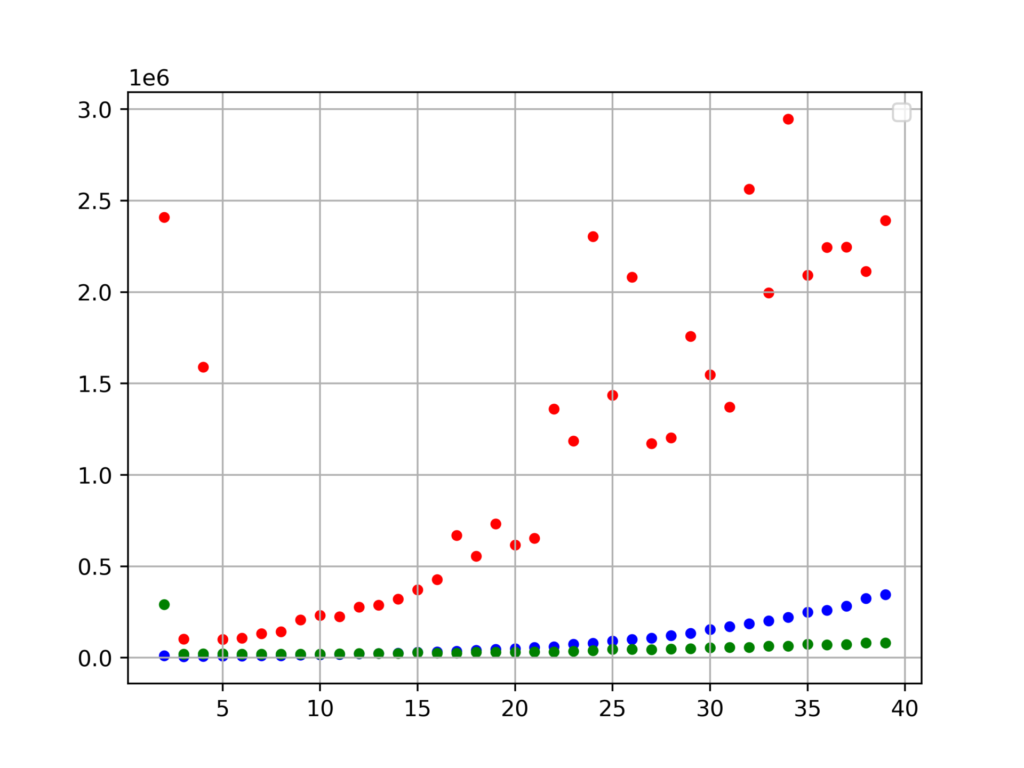
頭おかしいですね。これからはビルトインメソッドを使います。



