統計を勉強している時にモンテカルロ法という方法を見つけましたが、この方法を使えばあらゆる面積比を出せそうなので、積分近似に応用してみたいと思います。
目次
高校数学の定積分
高校数学で出てきた基礎的な定積分の答えを、通常の手計算とモンテカルロ法で解いてみます。
以下のような定積分について考えます。
$$\int_{0}^{2}e^{x}sinxdx$$
手計算での定積分
部分積分方を利用すると
$$\begin{align}I&=\int e^{x}sinxdx \\&=e^x(sinx-cosx) – \int e^{x}sinxdx\\&\therefore \int e^{x}sinxdx= \frac{e^x(sinx-cosx)}{2}\end{align}$$
よって、
$$\begin{align}\int_{0}^{2}e^{x}sinxdx&= \frac{e^2(sin2-cos2)+1}{2}\\&\simeq 5.39\end{align}$$
モンテカルロ法での計算
初めに、視覚的に理解しやすいようにグラフを描画します。
import matplotlib.pyplot as plt
import numpy as np
import sympy as sp
fig = plt.figure()
plt.xlabel('x')
plt.ylabel('f(x)')
plt.grid()
x = np.linspace(-1,3,10000)
f = np.exp(x)*np.sin(x)
plt.scatter(x,f,s=1)
fig.savefig('result.png',dpi=500)出力結果
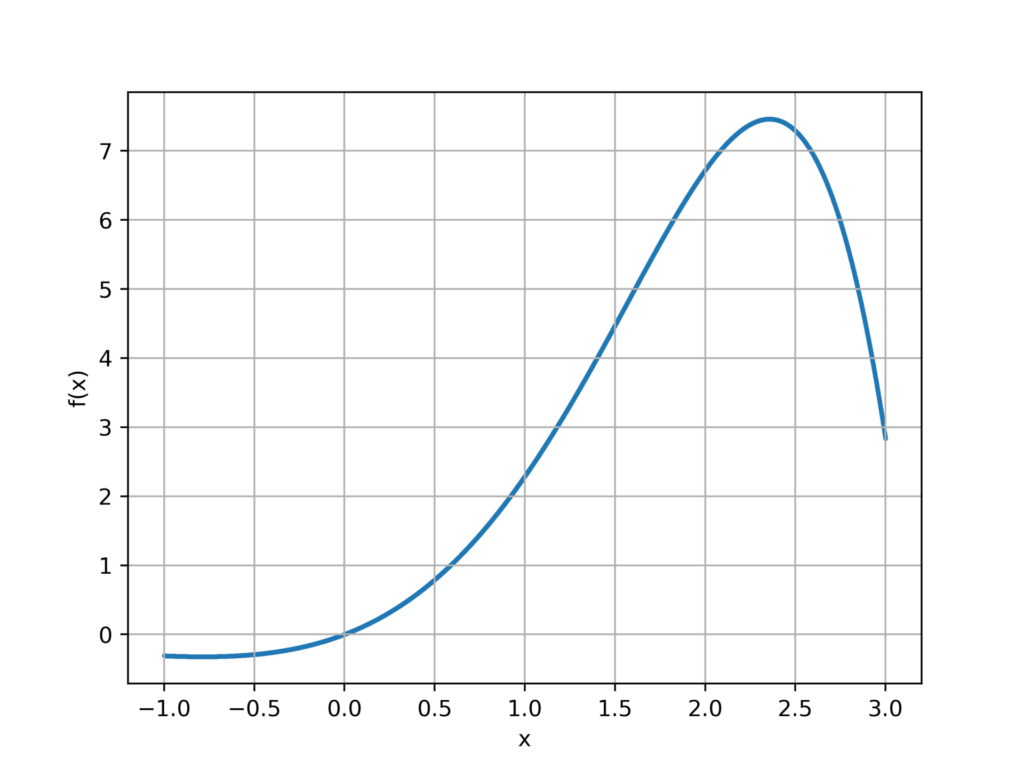
ここで、積分範囲を囲む四角形を生成してみます。
import matplotlib.pyplot as plt
import numpy as np
import sympy as sp
fig = plt.figure()
plt.xlabel('x')
plt.ylabel('f(x)')
plt.grid()
plt.hlines(7,0,2,color="red")
plt.hlines(0,0,2,color="red")
plt.vlines(0,0,7,color="red")
plt.vlines(2,0,7,color="red")
x = np.linspace(-1,3,10000)
f = np.exp(x)*np.sin(x)
plt.scatter(x,f,s=1)
plt.fill_between(x,f,color='blue',alpha=0.09)
fig.savefig('result.png',dpi=500)出力結果
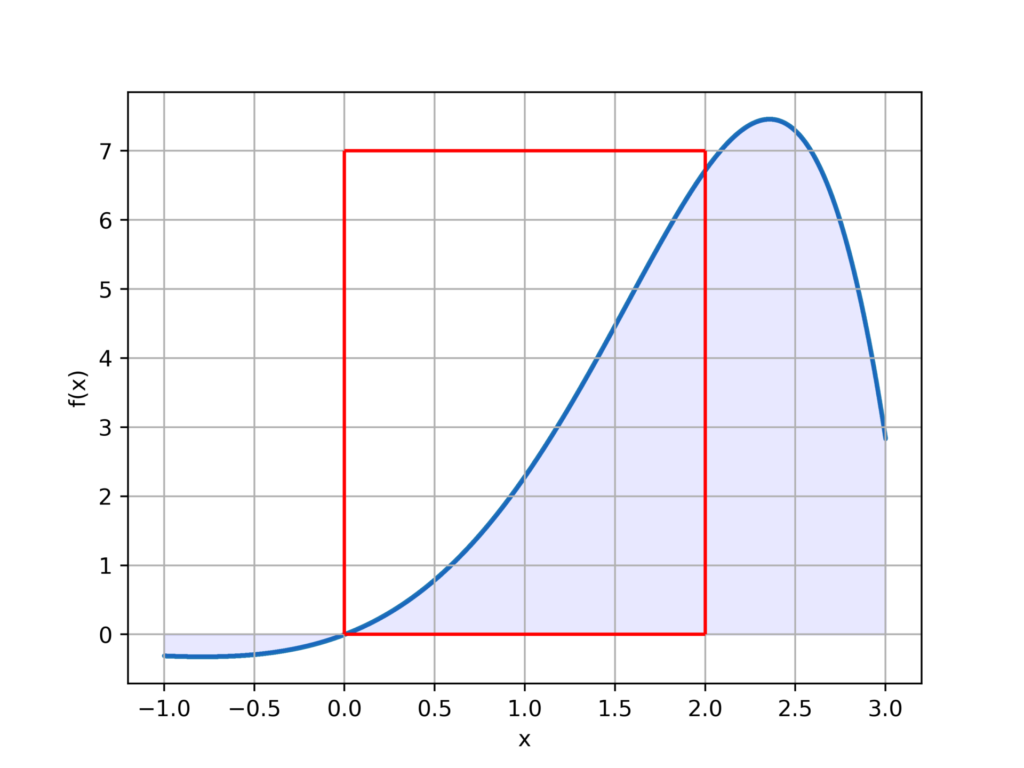
赤枠の面積をS,積分領域をIとすると、面積比は当然
$$A=\frac{I}{S}$$
となります。
この垢枠の内側にランダムプロットを行い、積分領域に入ったものとそれ以外のものの割合から積分値を求めてみます。
以下のようなアルゴリズムを作成し、n=100で積分の近似値を出力しました。
同時にランダムプロットを可視化しています。
from itertools import count
from random import random
from tkinter import YView
from turtle import color
import matplotlib.pyplot as plt
import numpy as np
from pkg_resources import yield_lines
import sympy as sp
import random
fig = plt.figure()
plt.xlabel('x')
plt.ylabel('f(x)')
plt.grid()
plt.hlines(7,0,2,color="red")
plt.hlines(0,0,2,color="red")
plt.vlines(0,0,7,color="red")
plt.vlines(2,0,7,color="red")
x = np.linspace(-1,3,10000)
f = np.exp(x)*np.sin(x)
plt.scatter(x,f,s=1)
plt.fill_between(x,f,color='blue',alpha=0.09)
n = 100
counter = 0
for i in range(n):
x_r = random.uniform(0,2)
y_r = random.uniform(0,7)
if np.exp(x_r)*np.sin(x_r) > y_r:
counter+= 1
plt.scatter(x_r,y_r,s=1,color='red')
else:
plt.scatter(x_r,y_r,s=1,color='blue')
print(counter/n*14)
fig.savefig('result.png',dpi=500)出力結果
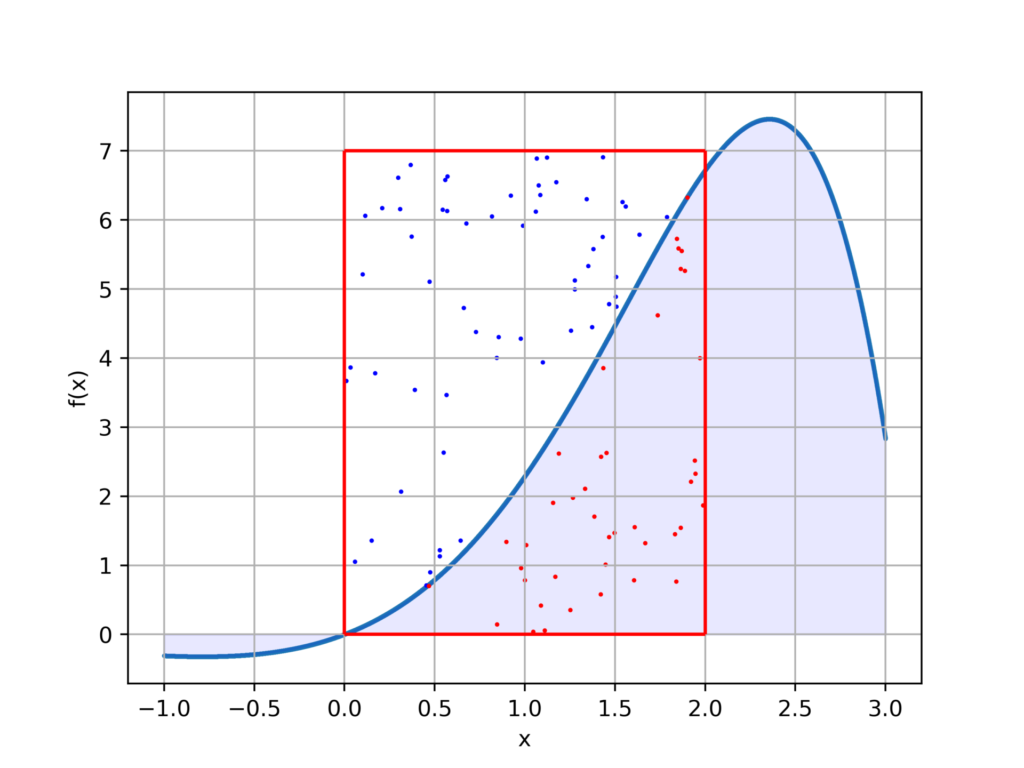
5.7399nを10000に増やしてみた出力結果
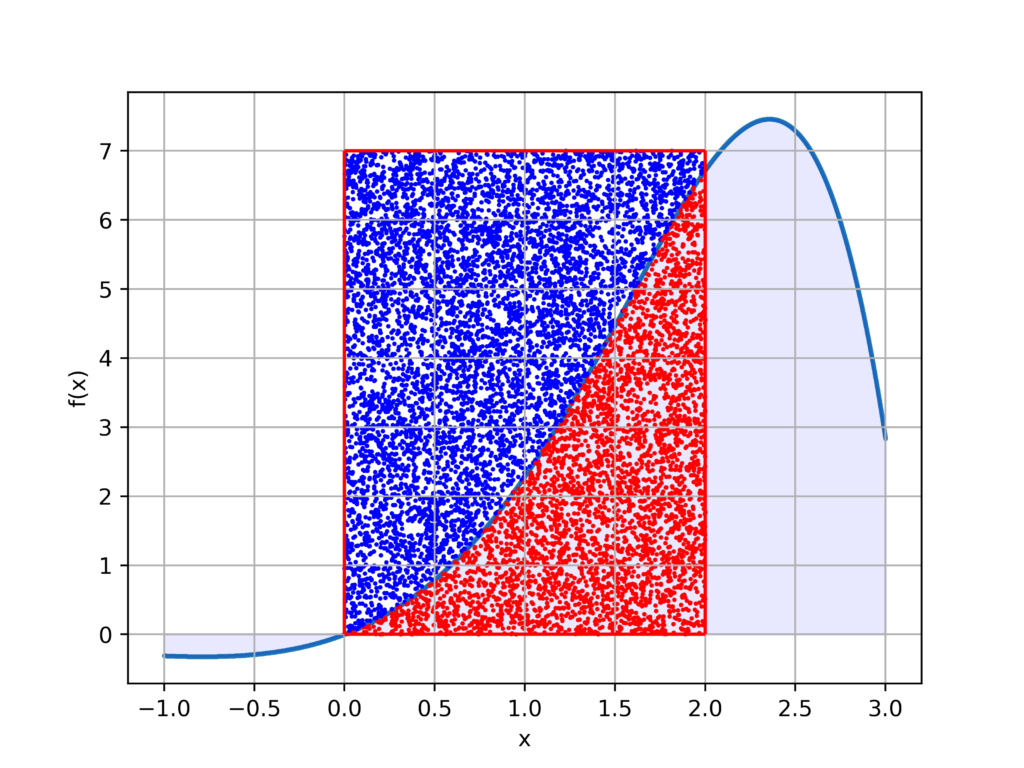
5.3046実際の積分値に近似できていることがわかります。
初等関数で表せない関数の積分近似
以下の定積分について考えてみます。
$$\int_{0}^{1}e^{x^2}dx$$
この関数は一見不定積分が出せそうで出せません。もちろん、初等関数以外を用いれば表すことはできますが、手計算ではおそらく大変時間がかかります。
この定積分に関して、sympyでの計算結果とモンテカルロ法での計算結果を比べてみたいと思います。
sympyでの計算結果
以下のようにして定積分を計算します。
import sympy as sp
import numpy as np
sp.init_printing(use_unicode=True)
x = sp.symbols("x")
f = sp.exp(x**2)
print(sp.integrate(f,(x,0,1)).evalf())
>>>
1.46265174590718モンテカルロ法での計算結果
初めに、グラフを描画しプロット領域を決定します。
import matplotlib.pyplot as plt
import numpy as np
import sympy as sp
import random
from tqdm import tqdm
fig = plt.figure()
plt.xlabel('x')
plt.ylabel('f(x)')
plt.grid()
plt.hlines(3,0,1,color="red")
plt.hlines(0,0,1,color="red")
plt.vlines(0,0,3,color="red")
plt.vlines(1,0,3,color="red")
x = np.linspace(-0.5,1.3,10000)
f = np.exp(x**2)
plt.scatter(x,f,s=1)
plt.fill_between(x,f,color='blue',alpha=0.09)
fig.savefig('result.png',dpi=500)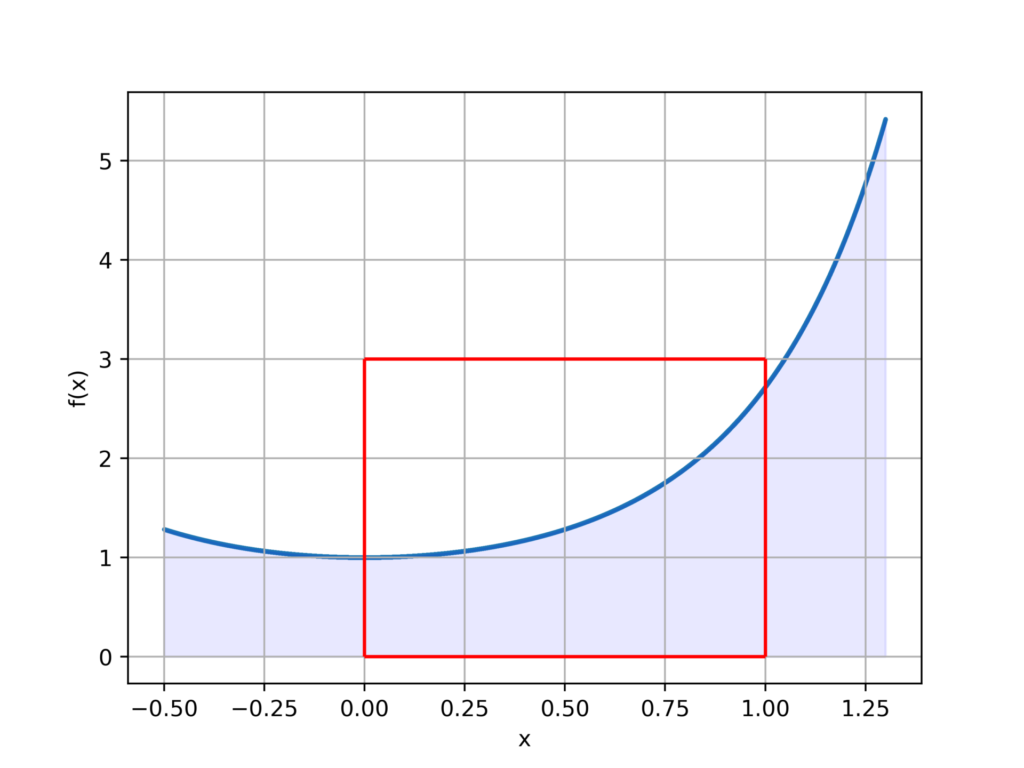
この領域内にランダムプロットを行っていきます。
def get_fraction(n):
counter = 0
for i in tqdm(range(n)):
x_r = random.uniform(0,1)
y_r = random.uniform(0,3)
if np.exp(x_r**2) > y_r:
counter+= 1
plt.scatter(x_r,y_r,s=1,color='red')
else:
plt.scatter(x_r,y_r,s=1,color='blue')
pass
return counter/n
print(get_fraction(100)*3)
fig.savefig('result.png',dpi=500)
>>>
1.26出力結果
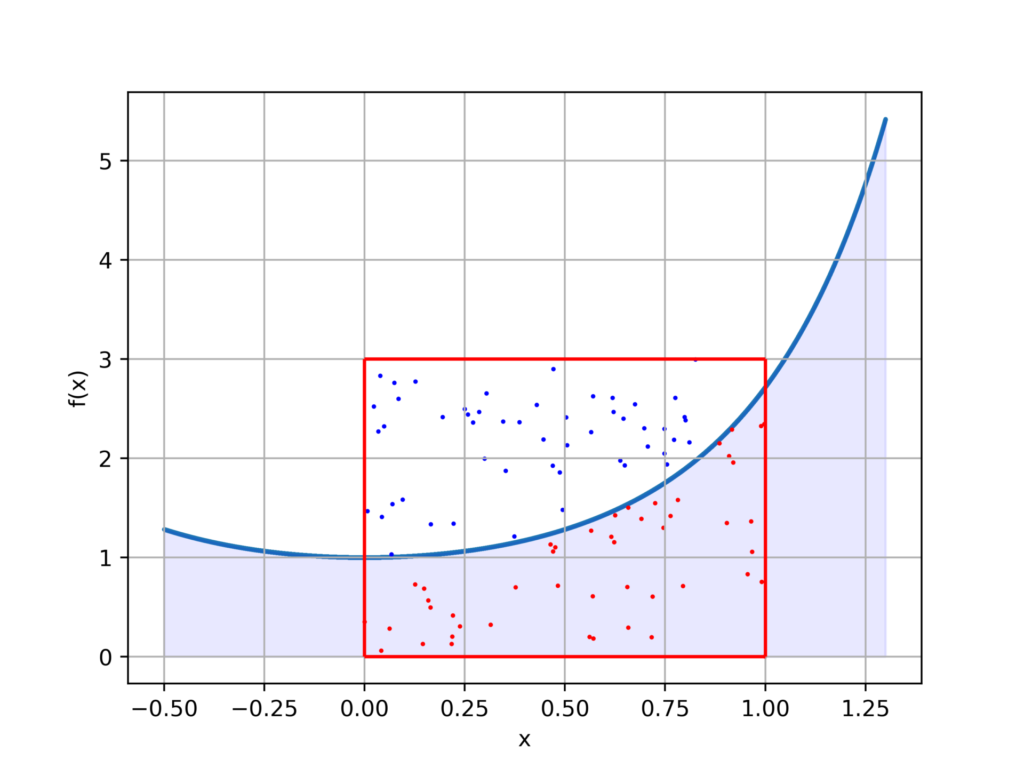
nを10000まで増やします。
print(get_fraction(100)*3)
>>>
1.4577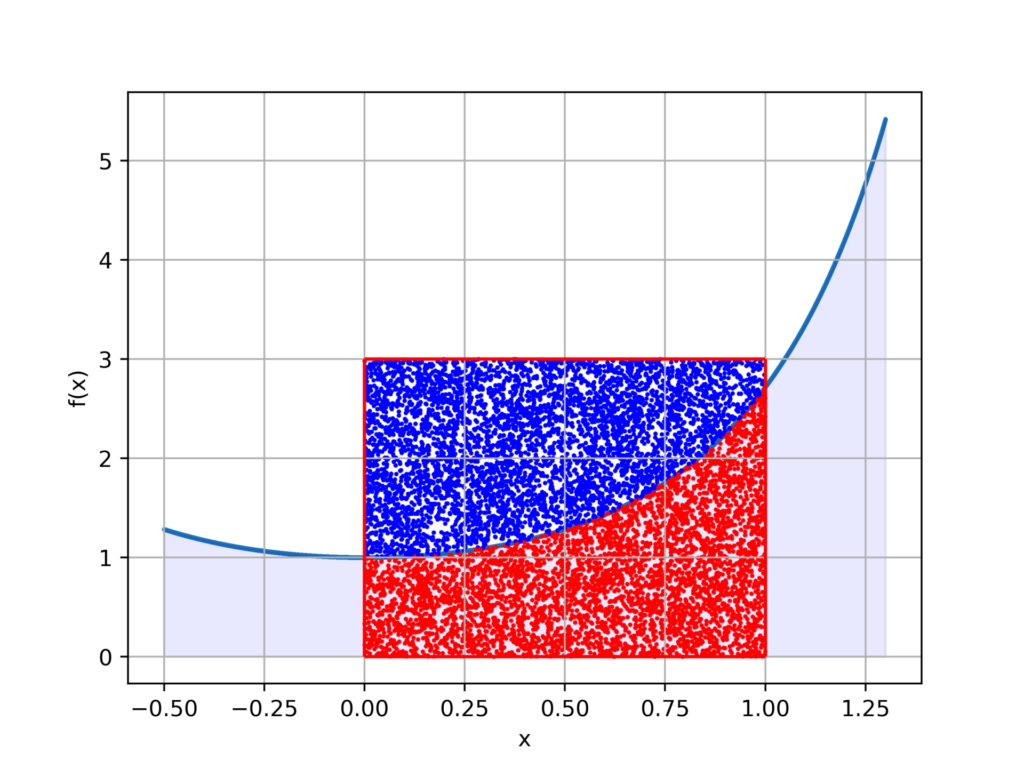
nが増えれば増えるほど、実際の面積比に近づくことがわかります。



