カイ二乗分布 【Pythonで学ぶ統計】

カイ二乗分布 とは

母数k(自由度）のカイ二乗分布は以下のように定義されます。

確率変数Xが標準正規分布に従う時、

$$Z\sim\chi^2=\sum_{i=1}{k} {X_i}^2$$

言葉で言い換えると、標準正規分布に従う確率変数の二乗和が従う分布のことです。

確率密度関数

母数kの時、カイ二乗分布の確率密度関数は以下のように表されます。

$$f(x;k)=\left\{\begin{array}{ll}\dfrac{x^{\frac{k}{2}-1}e^{-\frac{x}{2}}}{2^{\frac{k}{2}}\Gamma (\frac{k}{2})}&(\forall{x}\geq 0)\\0&(\forall x<0)\end{array}\right.$$

このうち、ガンマ関数は以下のように表されます。

$$\begin{align}\displaystyle \Gamma (z)&= \int_0^{\infty}t^{z-1}e^{-t}dt \quad ( z \in \mathbb{C}, \, \Re z>0 )\\&=\int_0^{\infty}t^{\frac{k}{2}-1}e^{-\frac{k}{2}}dt \quad\end{align}$$

pythonでプロット

自由度4までの場合

pythoを使用してカイ二乗分布をプロットしてみます。

import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import chi2 as stats
fig = plt.figure()
plt.xlabel('x')
plt.ylabel('PDF_chi')
plt.xlim(0, 10)
plt.ylim(0, 1.0)
plt.grid()
x = np.linspace(0, 10, 1000)

linestyles = [':', '--', '-.', '-']
df = [1, 2, 3, 4]
for k, ls in zip(df, linestyles):
  plt.plot(x, stats.pdf(x, k), linestyle=ls, label='k={}'.format(k))

plt.legend()
fig.savefig('result_chi.png',dpi=500)

自由度kまでの拡張

以下のようにして、任意の自由度までのカイ二乗分布をプロットするコードに書き換えます。

import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import chi2 as stats

n = 17
fig = plt.figure()
plt.xlabel('x')
plt.ylabel('PDF_chi')
plt.xlim(0, 50)
plt.ylim(0, 1.0)
plt.grid()
x = np.linspace(0, 50, 1000)
df = [i for i in range(1,n+1)]
for k in df:
  plt.plot(x, stats.pdf(x, k), label='k={}'.format(k))
plt.legend()
fig.savefig('result_chi.png',dpi=500)

出力結果

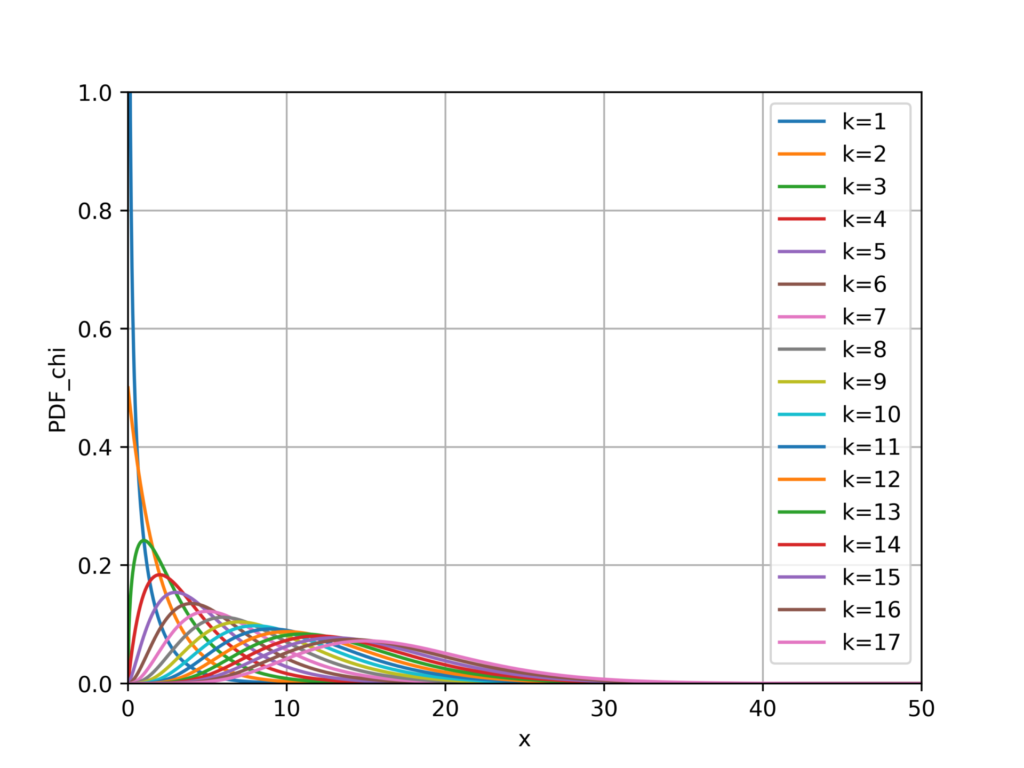
自由度17までのプロット結果です。

カイ二乗分布の期待値の導出

連続型確率変数において期待値E(X)は

$E(X)=\int_{-\infty}^{\infty}xf(x;k)dx$

この時、

$f(x;k)=\dfrac{x^{\frac{k}{2}-1}e^{-\frac{x}{2}}}{2^{\frac{k}{2}}\Gamma (\frac{k}{2})}\quad (\forall x \geq 0)$

より

$\begin{align}E(X)&=\int_{0}^{\infty}x\dfrac{x^{\frac{k}{2}-1}e^{-\frac{x}{2}}}{2^{\frac{k}{2}}\Gamma (\frac{k}{2})}dx\quad(\Gamma(k)=(k-1)\Gamma(k-1))\\&=\int_{0}^{\infty}\dfrac{x^{\frac{k}{2}}e^{-\frac{x}{2}}}{2^{\frac{k}{2}}\Gamma (\frac{k}{2})}dx\\&=\int_{0}^{\infty}\dfrac{x^{k’-1}e^{-\frac{x}{2}}}{2^{k’}2^{-1}(\frac{k}{2})^{-1}\Gamma (k’)}dx\\&=k\int_{0}^{\infty}\dfrac{x^{k’-1}e^{-\frac{x}{2}}}{2^{k’}\Gamma (k’)}dx\\&=k\end{align}$

カイ二乗検定

カイ二乗検定