大数の法則は以下のように定義されます。
例えば平均μを持つn個の確率変数列について、標本平均を以下のように定義するときについて考えます。
$$\bar{X_n}=\frac{1}{n}\sum_{i=1}^{n}X_i$$
この時、以下の式が成り立ちます。
$$\lim_{n \to \infty}P(|\bar{X_n}-\mu|>\epsilon)=0,\forall{\epsilon}>0$$
これを大数の弱法則と言います。
目次
大数の弱法則
以下のチェビシェフの不等式を利用すると、
$$P(|X-\mu|)\geq k\sigma)\leq \frac{1}{k^2},\forall{k}>1$$
$$\begin{align}&P(|\sum_{i=1}^{n}X_i-n\mu|>n\epsilon)\\&\leq \frac{E[|\sum_{i=1}^{n}X_i-n\mu|^2]}{n^2\epsilon ^2}\\&=\frac{V(\sum_{i=1}^{n}X_i)}{n^2\epsilon ^2}\end{align}$$
確率変数は独立であるから
$$V(\sum_{i=1}^{n}X_i)=n\sigma^2$$
より
$$P(|\bar{X_n}-\mu|>\epsilon)≤\frac{n\sigma^2}{n^2\epsilon ^2}=\frac{\sigma^2}{n\epsilon ^2}$$
極限をとると
$$0≤\lim_{n \to \infty}P(|\bar{X_n}-\mu|>\epsilon)≤\lim_{n \to \infty}\frac{\sigma^2}{n\epsilon ^2}=0$$
よって、
$$\lim_{n \to \infty}P(|\bar{X_n}-\mu|>\epsilon)=0,\forall{\epsilon}>0$$
が成り立ちます。
収束の様子をPythonで可視化
収束の様子をPythonで可視化してみようと思います。
まずはコインについて考えます。
裏を0,表を1とした時、μの理論値は0.5ですが、大数の法則に基づくとこの値に収束することが予想されます。
まずは50回コインを投げてみます。
import matplotlib.pyplot as plt
import random
fig = plt.figure()
plt.xlabel('Number of trials')
plt.ylabel('Average')
nums = 50
plt.xlim(0,nums)
plt.ylim(0,1)
X_i = [0,1]
front_num = 0
result = []
for i in range(1,nums):
X = random.choice(X_i)
if X == 1:
front_num+=1
else:
pass
result.append(front_num/i)
plt.plot([i for i in range(len(result))],result)
plt.plot([i for i in range(len(result))],[1/2 for i in range(len(result))])
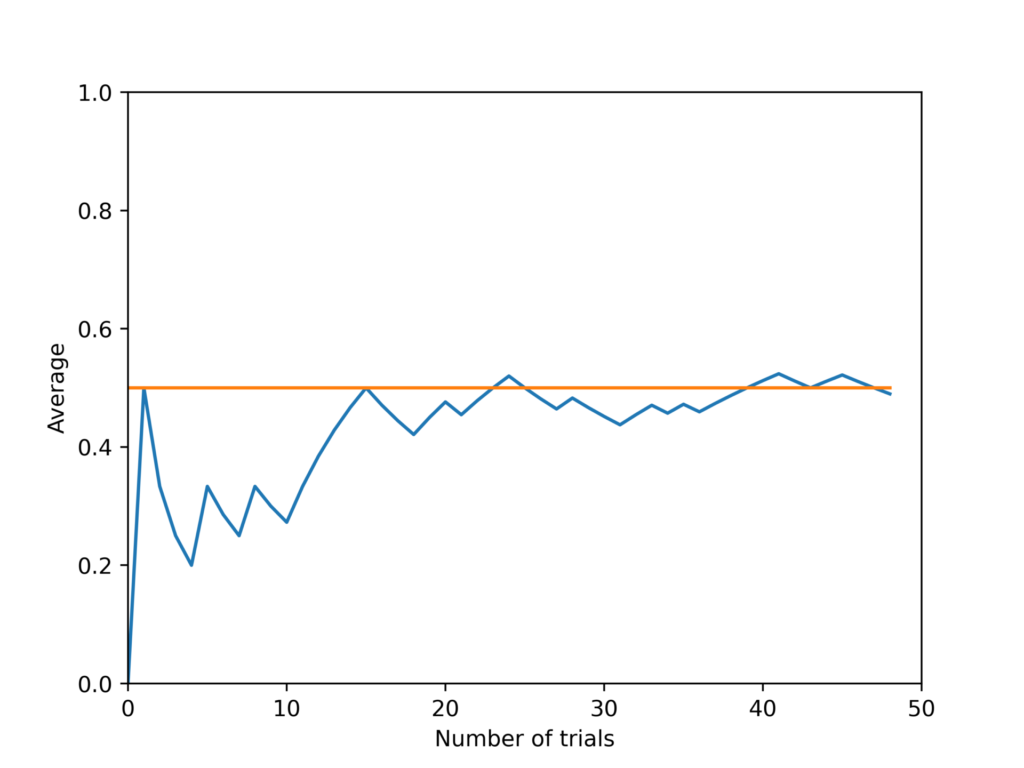
fig.savefig('result.png',dpi=500)実行結果
横軸が試行回数、縦軸がその平均です。オレンジ色のラインはy=0.5を著しています。
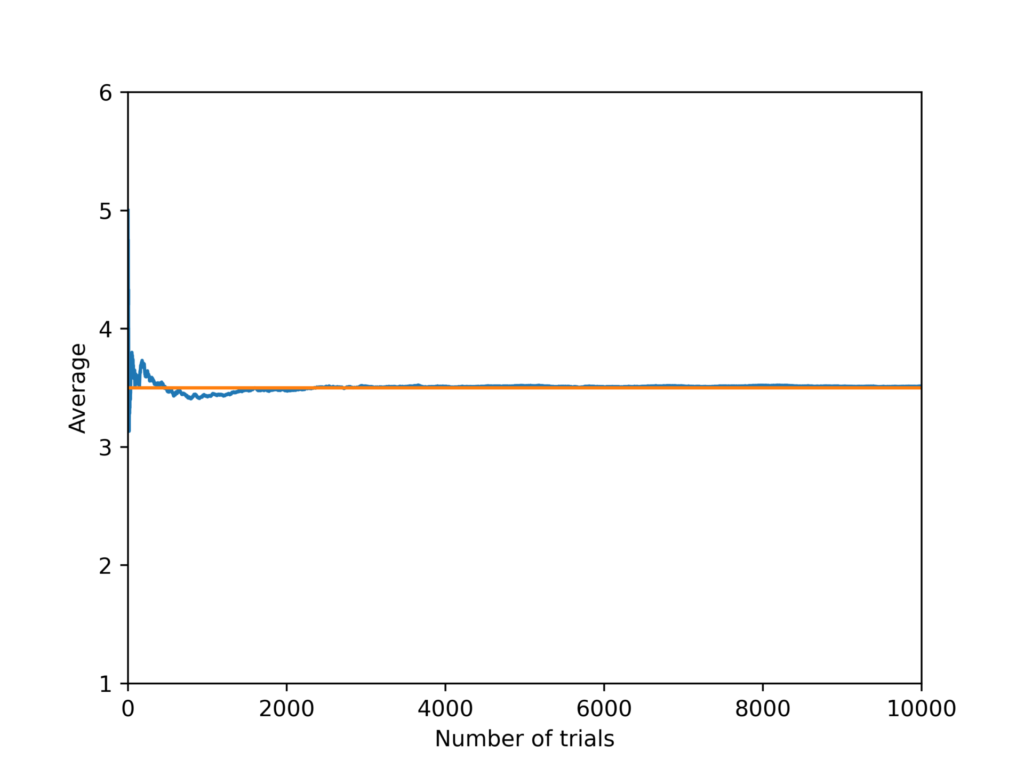
ループ回数を10000に上げてみます。
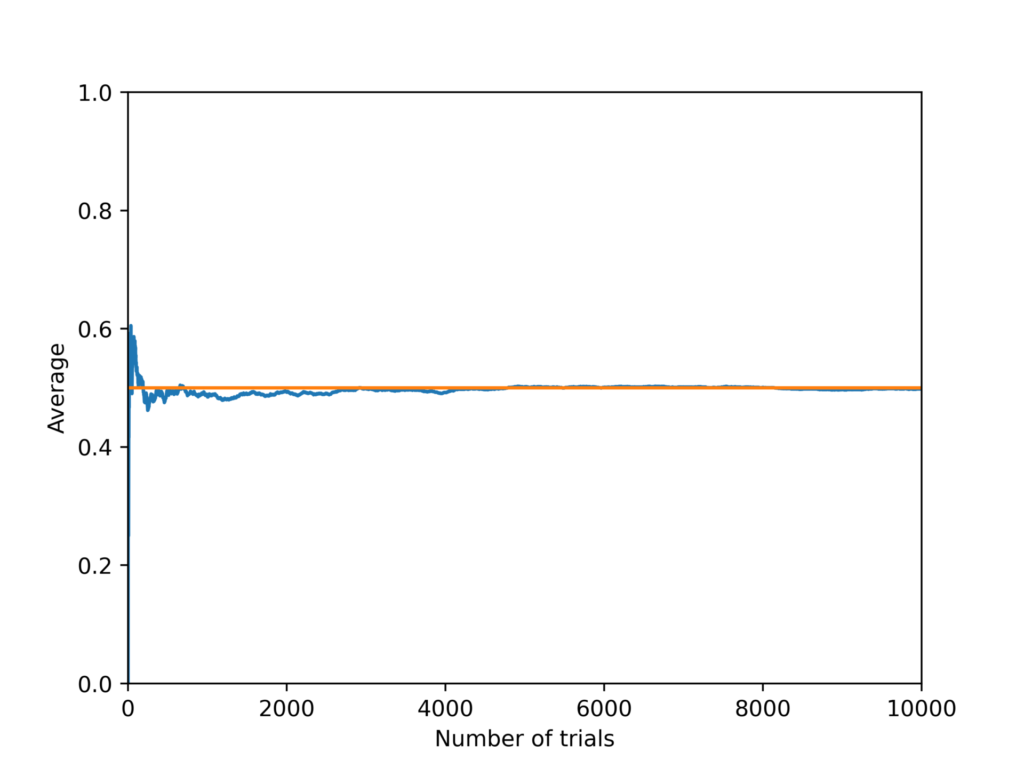
μの理論値に収束していく様子がわかります。
サイコロの場合
サイコロについても考えてみます。
少しコードを書き換えました。
import matplotlib.pyplot as plt
import random
fig = plt.figure()
plt.xlabel('Number of trials')
plt.ylabel('Average')
nums = 50
plt.xlim(0,nums)
plt.ylim(0,6)
X_i = [1,2,3,4,5,6]
front_num = 0
result = []
for i in range(1,nums):
front_num+=random.choice(X_i)
result.append(front_num/i)
plt.plot([i for i in range(len(result))],result)
plt.plot([i for i in range(len(result))],[sum(X_i)/len(X_i) for i in range(len(result))])
fig.savefig('result.png',dpi=500)50回の場合
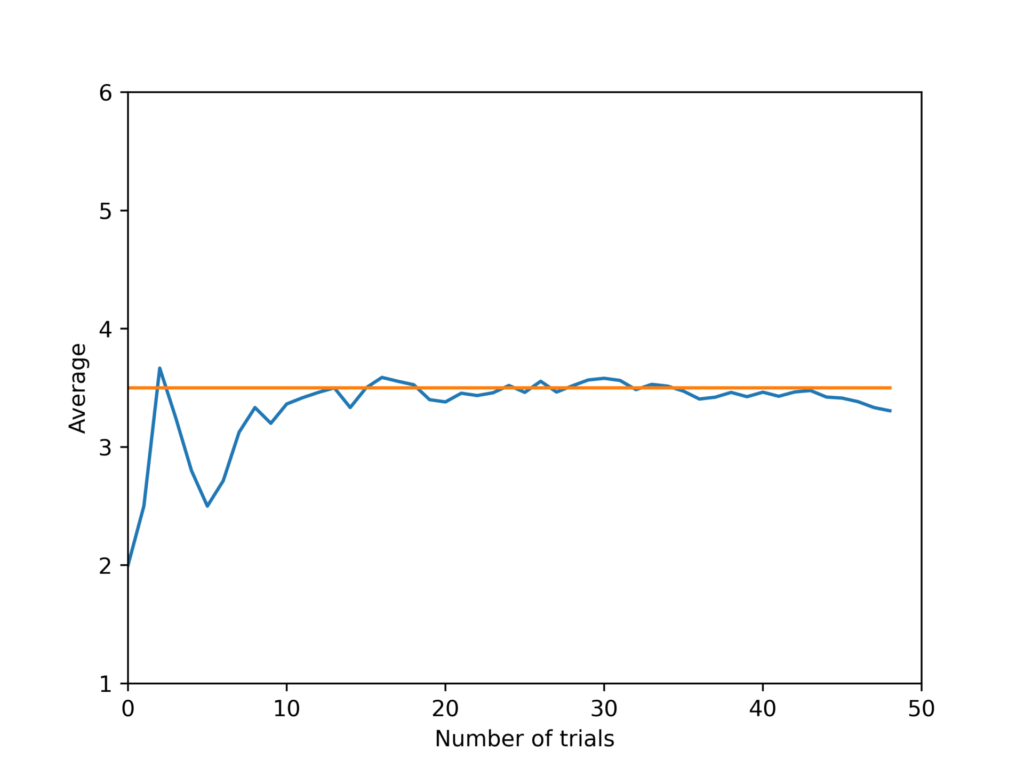
10000回の場合