チェビシェフの不等式 【Pythonで学ぶ統計】

確率論の基本的な定理の一つにチェビシェフの不等式があります。

定義

期待値μ,標準偏差σをもつ確率変数Xについて、

$$P(|X-\mu|\geq k\sigma)\leq \frac{1}{k^2},\forall{k}>1,k\in\mathbb{R}$$

および余事象

$$P(|X-\mu|< k\sigma)>1- \frac{1}{k^2},\forall{k}>1,k\in\mathbb{R}$$

が成り立つ。

例えばk=2の時、分散および期待値がわかっている確率変数の集合に対して、少なくとも75%の確率変数は区間$$(\mu-2\sigma,\mu+2\sigma)$$に含まれるということができる。

また、平均μ,標準偏差σが与えられるあるデータについて、半分のデータがどの範囲に含まれるか知りたい場合について考えると、

$$k=\sqrt{2}$$

であり、

半分のデータが存在する区間は

$$(\mu-\sqrt{2}\sigma,\mu+\sqrt{2}\sigma)$$

であると言える。

具体例

例えば、平均1000kbp,標準偏差100kbpの塩基配列データがあるとする。

この時、チェビシェフの不等式から

ということがわかる。

Pythonで可視化

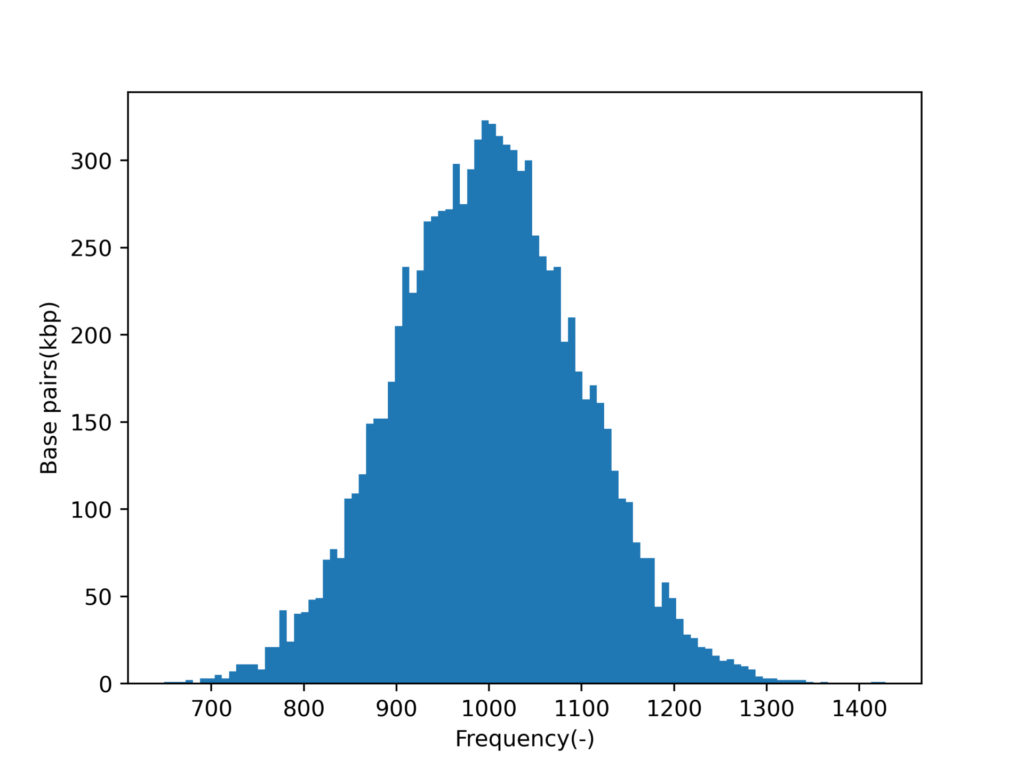
まずは標準偏差100kbp,平均1000kbpの塩基配列データを10000個生成し、ヒストグラムにしてみます。

import numpy as np
import matplotlib.pyplot as plt
fig = plt.figure()
PDF = np.random.normal(1000, 100, 10000)
plt.hist(x, bins=100)
plt.xlabel('Frequency(-)')
plt.ylabel('Base pairs(kbp)')
filename="hist2.png"
plt.savefig(filename)
fig.savefig('result.png',dpi=500)

実行結果

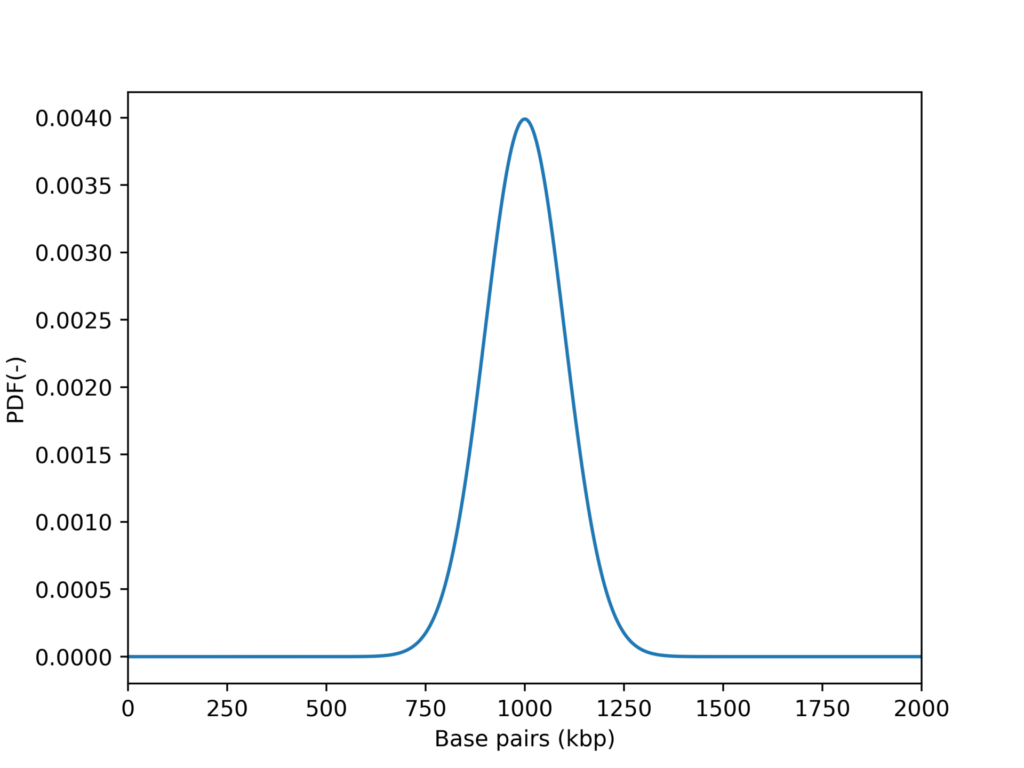
正規分布曲線を描いてみます。

import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import norm
import math

fig = plt.figure()
x = np.arange(0,2000,0.1)
PDF =  norm.pdf(x,1000,100)
plt.plot(x,PDF)
plt.xlabel('Frequency(-)')
plt.ylabel('PDF(-)')
plt.xlim(0,2000)
fig.savefig('result.png',dpi=500)

実行結果

ここで、k=2の場合について考えてみます。

k=2の時、全体の少なくとも75%は800kbpから1200kbpに存在するということを証明するために、この区間で確率密度関数を積分してみます。

import sympy as sp 
sp.init_printing(use_unicode=True)
x = sp.symbols("x")
sigma = 100
mu = 1000
PDF = (1/(sp.sqrt(2*sp.pi*sigma**2)))*sp.exp(-(((x-mu)**2)/(2*sigma**2)))

integral = sp.integrate(PDF,(x,800,1200)).evalf()

print(integral)

実行結果

0.954499736103642

不等式が成り立っていることがわかります。

k=nへの拡張

チェビシェフの不等式が成り立つかどうかを確かめるために、以下のようなアルゴリズムを考えます。

$\begin{align}&for\quad i(\forall{k}>1):\\&IF\quad P(|X-\mu|)\geq k\sigma)\leq \frac{1}{k^2}\end{align}$

コードに落とし込むと、以下のようになります。

import sympy as sp 
sp.init_printing(use_unicode=True)
x = sp.symbols("x")
sigma = 100
mu = 1000
PDF = (1/(sp.sqrt(2*sp.pi*sigma**2)))*sp.exp(-(((x-mu)**2)/(2*sigma**2)))
valiation = True
for k in range(2,100,1):
    if sp.integrate(PDF,(x,mu-k*sigma,mu+k*sigma)).evalf()> 1/k**2:
        pass 
    else:
        valiation = False 
if valiation:
    print(True)

実行結果

True

不等式の証明

チェビシェフの不等式を証明するには、以下のマルコフ不等式を使用します。

ここで、期待値の性質から

$$P(|X|^2\geq a^2 )\leq\frac{E[|X|^2]}{a^2}$$

が成り立つことから、

$$X=X-\mu,a=k\sigma$$

のもとで

$$P(|X-\mu|\geq k\sigma)\leq \frac{E[|X-\mu|^2]}{k^2\sigma^2}$$

分散に関して

$$\begin{align}V(X)&=E(X^2)-{E(X)}^2\\&=E[|X-\mu|^2]\end{align}$$

であるから、

$$P(|X-\mu|)\geq k\sigma)\leq \frac{1}{k^2}$$

を得る。