正規分布について 【Pythonで学ぶ統計】

正規分布とは、以下の確率密度関数f(x)で与えられる確率分布です。

$$f(x;\mu,\sigma^2)=\dfrac{1}{\sqrt{2\pi\sigma}}\exp(-\dfrac{(x-\mu)^ 2}{2\sigma^ 2})(x\in\mathbb{R})$$

自然現象は正規分布に従うことが多いため、統計学では非常に重要な項目なようです。

正規分布のグラフ

式からわかるように、正規分布のグラフの形は平均μと標準偏差σで決まります。

平均は正規分布のグラフの凸部の位置を、標準偏差がグラフの凸部の幅を決めます。

pythonを使って正規分布を可視化してみます。

標準偏差を20,平均を50にしてプロットしてみます。

import numpy as np
from scipy.stats import norm
import math
import matplotlib.pyplot as plt
fig = plt.figure()
mu = 50
sigma = 20
X = np.arange(0,100,0.1)
Y = norm.pdf(X,mu,sigma)
plt.plot(X,Y)
fig.savefig('result.png',dpi=500)

実行結果

正規分布の特徴

正規分布の大きな特徴は、平均値を中心として左右対称であるという点です。

グラフの山のような形は平均値や標準偏差がどの様な形をとっても保たれたままです。

また、確率密度関数の極限を考えると

$$\lim_{n \to \infty}f(x;\mu,\sigma^2)=\lim_{n \to -\infty}f(x;\mu,\sigma^2)=0$$

であることから、y=0に漸近することがわかります。

標準正規分布

正規分布の中には、標準正規分布と呼ばれる平均0,標準偏差1である特別な分布があります。

標準正規分布の確率密度関数を式で表すと

$$f(x;0,1)=N(0,1)=\dfrac{1}{\sqrt{2\pi}}\exp(-\dfrac{x^ 2}{2})$$

となります。

このグラフをプロットしてみます。

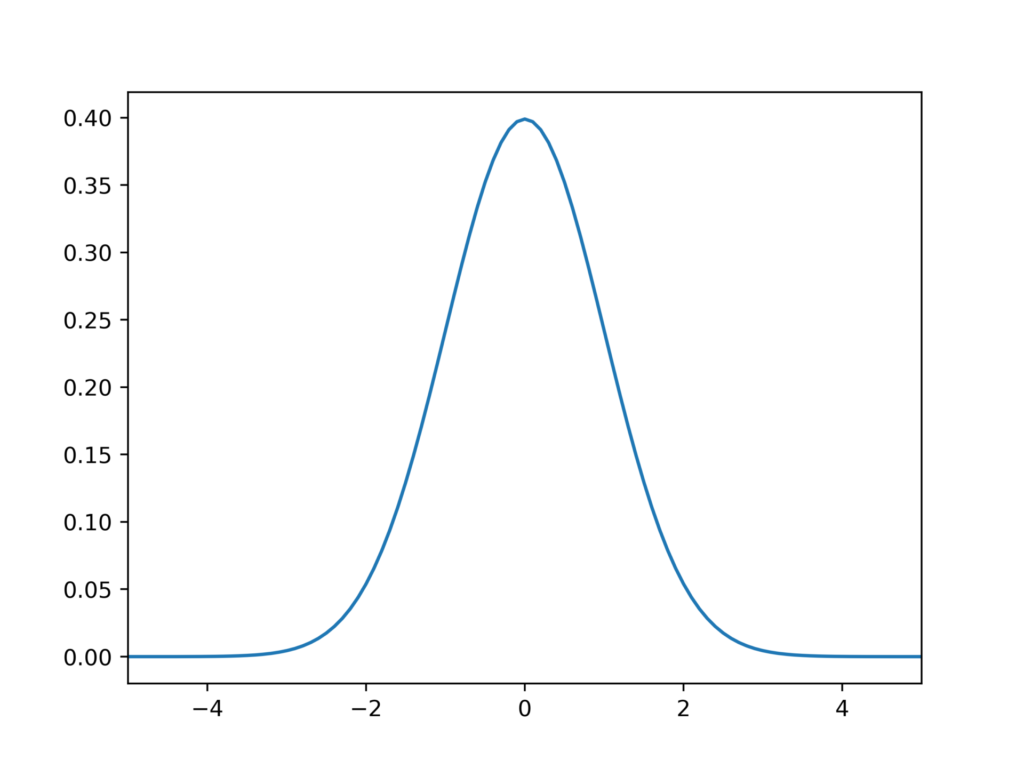
標準正規分布の良いところ

標準正規分布がどうしてわざわざ定義されているのかというと、どのような正規分布でも標準化することで標準正規分布に持っていくことができるという利点があるからです。

正規分布の標準化

早速、正規分布を標準化していきます。

確率変数が正規分布に従うとき、

$$Z = \frac{X-\mu}{\sigma}$$

となるZを定義すると、Zは平均μ,標準偏差σの正規分布に従います。

つまり、どのような正規分布でもZを使用して標準化できます。

例えば、確率変数Xが平均μ,標準偏差σの正規分布に従う時、A≤X≤Bとなる確率は、

$$Z = \frac{X-\mu}{\sigma}$$

より

$$P(\frac{A-\mu}{\sigma}≤Z≤ \frac{B-\mu}{\sigma})$$

となり、これは標準正規分布表から求めることができます。

Pythonでの実装

実際にPythonで積分してみます。

例えば、標準偏差10,平均20の標準偏差に従う正規分布について、10≤X≤20である確率を標準化を用いて求めると、

$$10≤X≤20→ 0≤Z≤0.5$$

より

$$P(0≤Z≤0.5)=\int_{a}^{b} f(x;\mu,\sigma)dx$$

標準正規分布であるから、

$$P(0≤Z≤0.5)=\int_{0}^{\frac{1}{2}}\dfrac{1}{\sqrt{2\pi}}\exp(-\dfrac{x^ 2}{2})dx$$

pythonで以下のように計算します。

import sympy as sp 
import numpy as np 
sp.init_printing(use_unicode=True)
x = sp.symbols("x")
sigma = 10
mu = 20
A = 10
B = 20
a,b = (A-mu)/sigma,(B-mu)/sigma
f = 1/(sp.sqrt(np.pi*2))*sp.exp(-(x**2)/2)
print(sp.integrate(f,(x,a,b)).evalf())

計算結果

0.341344746068543

よって、求めたい確率Pは上記の値になるということがわかりました。