以下の記事で、正規分布について扱っていますが、この正規分布を用いた統計学の中で重要な定理があります。
中心極限定理の定義
標本抽出対象の母集団が正規分布に従わない場合でもサンプルサイズが十分に大きい場合、その平均値の分布は正規分布に近似できる。
目次
中心極限定理の例
定理だけ見てもイメージが湧かないため、中心極限定理の例を考えてPythonで実装してみたいと思います。
サイコロの場合
サイコロには6つの目がありますが、このサイコロを2回投げた平均をn回取る場合について考えてみたいと思います。
以下の様にpythonで実装し、ヒストグラムを出力します。
import matplotlib.pyplot as plt
import random
fig = plt.figure()
plt.xlabel('Frequency(-)')
plt.ylabel('PD(-)')
n = 100
def get_rand(dice):
return (random.choice(dice)+random.choice(dice))/2
result = [get_rand([1,2,3,4,5,6]) for i in range(int(n))]
plt.hist(result,width=0.3)
fig.savefig('result.png',dpi=500)まずは、実行回数n、2回の平均の結果です。
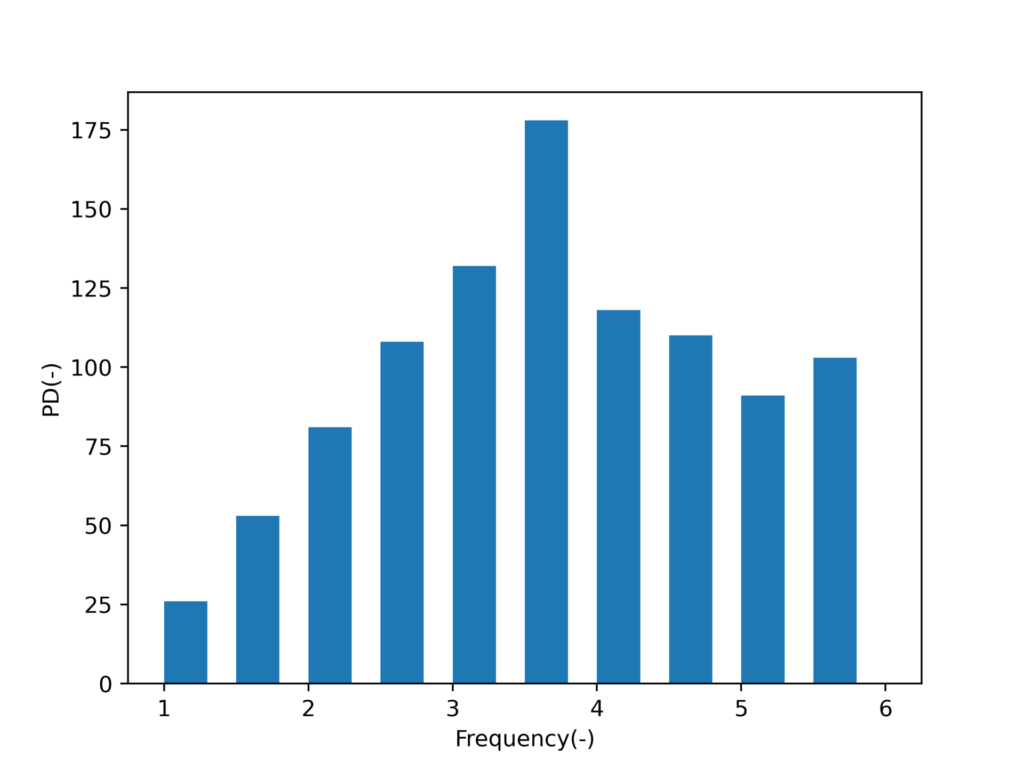
既に分布が正規分布に近づいてきているのがわかりますね。
次に、コードを以下の様に書き換えて平均を10回取ってみます。
import matplotlib.pyplot as plt
import random
fig = plt.figure()
plt.xlabel('Frequency(-)')
plt.ylabel('PD(-)')
plt.xlim(0,7)
n = 1000
m = 10
def get_rand(dice,m):
l = [random.choice(dice) for i in range(m)]
return sum(l)/(len(l))
result = [get_rand([1,2,3,4,5,6],m) for i in range(int(n))]
plt.hist(result,width=0.2)
fig.savefig('result.png',dpi=500)実行結果
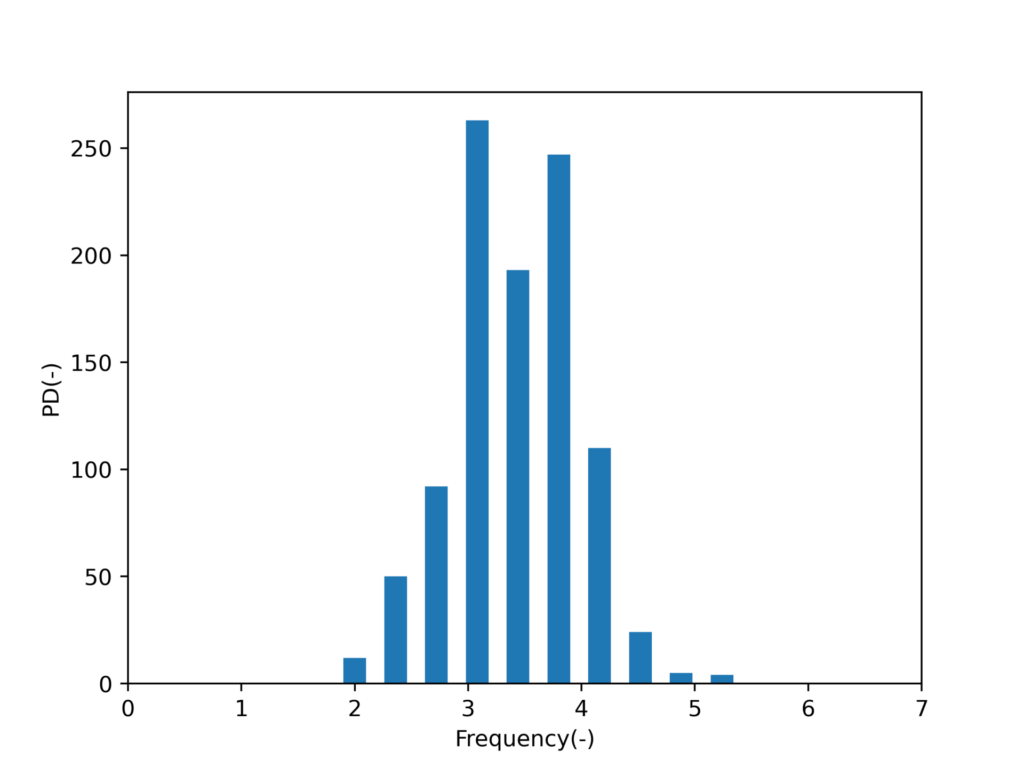
より正規分布に近くなってきています。
思い切ってm=1000にしてみるとどうでしょうか。
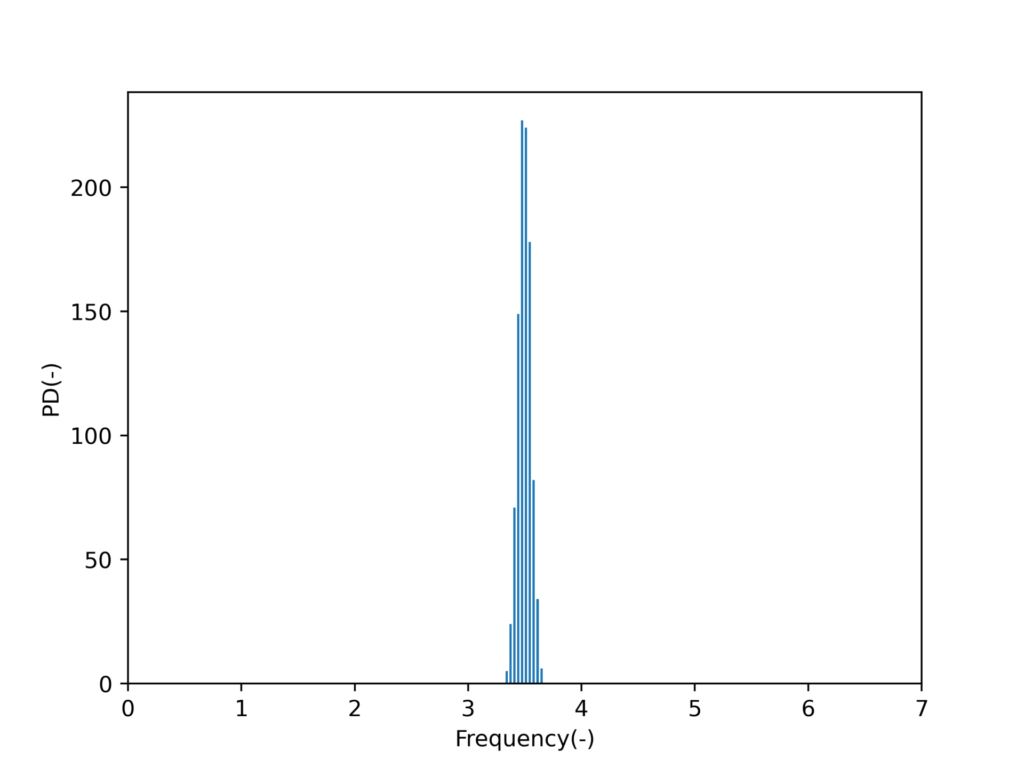
かなり正規分布に近付いていることがわかります。
中心極限定理の証明
サイコロに限らず、自然界の現象は十分な量のサンプリングを行うとその分布は正規分布に従うということが中心極限定理のコアとなります。このことを数学的に証明していきます。
まず、独立な確率変数Xiをn回繰り返すような場合を考えます。
この時、平均は
$$\bar{X}_n=\frac{1}{n}\sum_{i}^nX_i$$
と表されることは簡単にイメージできます。
勉強中なので書きかけです。


