確率密度関数と確率質量関数 【Pythonで学ぶ統計】

今回は、確率密度関数と確率質量関数の二つの違いについて勉強していきたいと思います。

確率密度関数とは

確率変数Xが連続的な値を取るときにXが閉区間(a≤X≤b)に含まれる確率Pとした時、以下の式におけるf(x)が確率密度関数となります。

$$P(a≤X≤b)=\int_{a}^{b}f(x)dx$$

確率変数が連続な場合の例として、例えば身長を測るとき、ちょうど170cmの人がいる確率はゼロになります。どう頑張っても下10桁くらいまで行けば絶対に170ちょうどとはならないことは、直感的にわかるかと思います。

そこで、169-171の間にある確率という考え方をしてあげれば、どんなに170ちょうどでなくても、その範囲に収まってくれる身長はたくさん出てくるため、確率分布の性質を反映させることができるのです。

また、式からわかるように、確率密度関数を区間で積分した結果、つまり面積が確率となります。

確率密度関数の性質

確率変数Xがとりうる値の範囲をA≤X≤Bとすれば、

$$P(A≤X≤B)=\int_{A}^{B}f(x)dx=1$$

となります。これは、離散型の確率変数の場合と同様で、確率を全て足し合わせると1になります。

また、確率密度関数には以下の様な性質もあります。

$$f(x)≥0$$

（確率密度関数は確率ではないため１を超えることもあります。）

正規分布

確率密度関数の例として、正規分布が挙げられます。

一般に、正規分布の確率密度関数は以下の様な式で与えられます。

$$f(x;\mu,\sigma^2)=\dfrac{1}{\sqrt{2\pi\sigma}}\exp(-\dfrac{(x-\mu)^ 2}{2\sigma^ 2})$$

母数μは平均、σは標準偏差を表しています。

正規分布に関しては他の記事で勉強していきます。

確率質量関数

確率密度関数は、確率変数が連続値の場合に適用できましたが、確率変数が離散型の場合はどうなるでしょうか。

例えば、サイコロは６つの目を持っていますが、それぞれの目が出る確率pは一意に決まっています。このような場合の確率分布を離散型確率分布と言います。

例えば、サイコロの目が1(x1)である確率をPとすれば、

$$P(X=x_1)=f(x_1)$$

より、確率質量関数はf(x1)であるといえます。

せっかくなのでmatplotlibを使って可視化してみようと思います。

import matplotlib.pyplot as plt 
fig = plt.figure()
x = ['x'+str(i+1) for i in range(6)]
y = [1/6 for i in range(len(x))]
plt.ylim(0,1)
plt.xlabel("X")
plt.ylabel('PMF(-)')
plt.bar(x,y,width=0.5)
fig.savefig('result.png',dpi=500)

出力結果

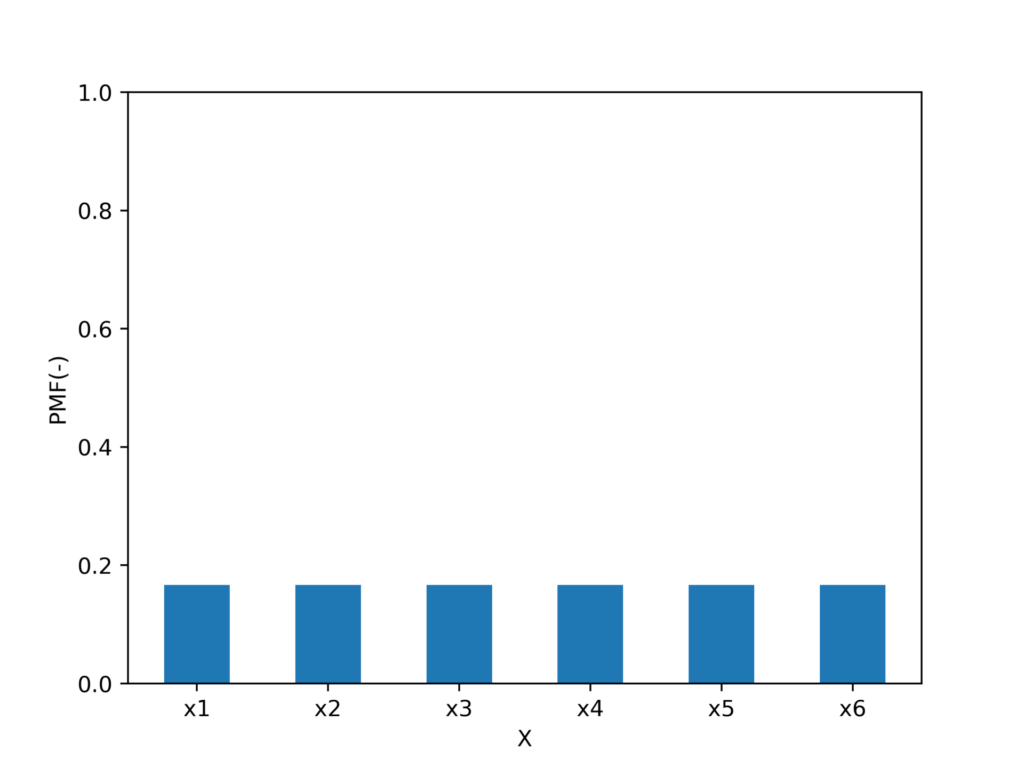
確率質量関数の性質

確率質量関数f(x)には以下の様な性質があります。

$$\sum_{x=1}f(x)=1,f(x)≥0$$