以前、極座標変換によって画像上の直線を検出する方法について考えました。
今回は、この方法を3次元空間まで拡張して円を検出する方法を考えていきます。
目次
3次元空間への射影
一般に円の方程式は以下のように表されます。
$$r^2 = R = (x-Cx)^{2}+(y-Cy)^{2}$$
つまり、円の定義を満たすには直交座標上のある一点(x,y)に対して3つのパラメータが存在することになります。
そのため、それぞれのパラメータをCx,Cy,R(r^2)とし3次元空間へ射影すると、(x,y)に固有の曲面ができることになります。
実際にプロットしてみます。
まずはいつも通り、モジュールをインポートしてインスタンスを生成します。
import matplotlib.pyplot as plt
import numpy as np
fig = plt.figure()
ax = fig.add_subplot( projection='3d')
ax.set_xlabel("Cx")
ax.set_ylabel("Cy")
ax.set_zlabel("r^2")今回は、直交座標上の点(5,3)を指定してパラメータの動向を見てみます。
また、円の中心の範囲を設定しないと無限の円が存在してしまうので、中心の領域を画像の大きさと同じ1920-1080としてみます。
x = 5
y = 3
x_max = 1920
y_max = 1080
Cx = np.linspace(0,x_max,70)
Cy = np.linspace(0,y_max,70)3次元空間に射影します。
R = (x-Cx)**2 + (y-Cy)**2
ax.scatter(Cx,Cy,R)
fig.savefig('circle.jpg',dpi = 500)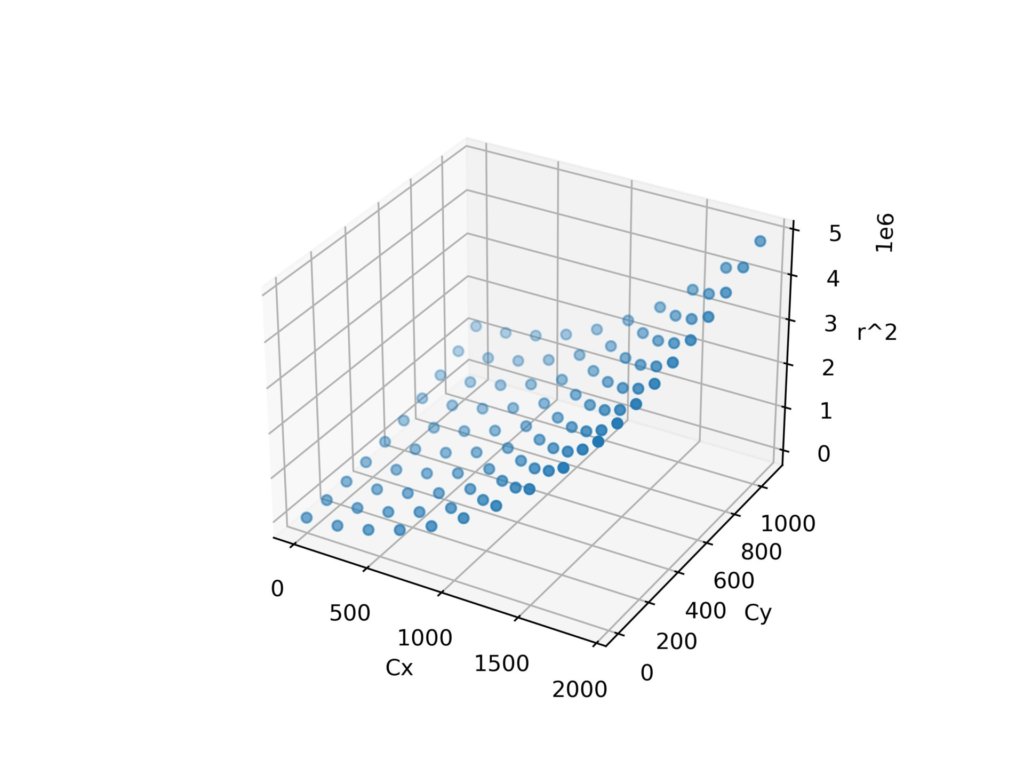
散布図では見にくいので、メッシュを生成します。
Cx,Cy = np.meshgrid(Cx,Cy)
R = (x-Cx)**2 + (y-Cy)**2
ax.plot_surface(Cx,Cy,R)見にくいですが、曲面ができているのがわかります。
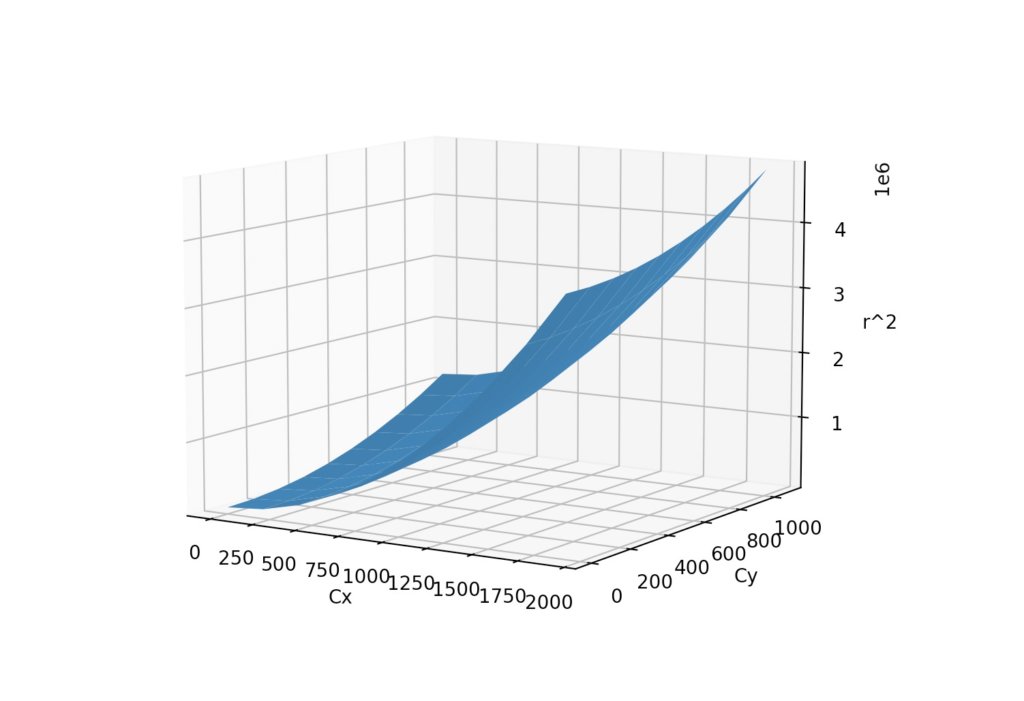
上記の曲面がCx,Cyの範囲における直交座標上の点(5,3)を三次元空間に写したものです。
円の検出
例えば、直交座標上にある4点を全て3次元空間に射影するとします。
この時、曲面同士が共有する点がわかると3つのパラメータを決定することができます。
そこで得られたパラメータを円の式に代入すると、直交座標上の4点全てを通る円の方程式を得ることができます。
この原理を応用することによって直交座標上の点からもっともらしい円を検出することができます。
x_max = 1920
y_max = 1080
Cx = np.linspace(0,x_max,10)
Cy = np.linspace(0,y_max,10)
Cx,Cy = np.meshgrid(Cx,Cy)
x = [250*i for i in range(4)]
y = [x[i]*3-100 for i in range(len(x))]
for i in range(len(x)):
R = (x[i]-Cx)**2 + (y[i]-Cy)**2
ax.scatter(Cx,Cy,R)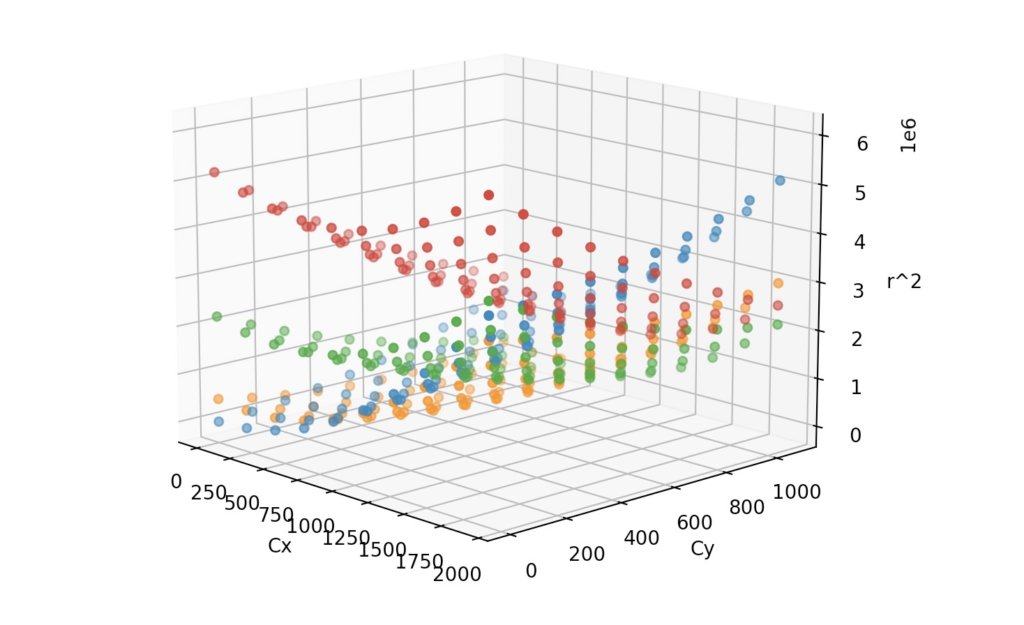
これらの曲面が交差している箇所を求めることによって、パラメータを決定することができます。



