前回の記事で、線形グラフ上のプロットを極座標変換して表した曲線を使用して直線の式を求めましたが、今回はランダムなプロットを生成してそれらの中からもっともらしい直線を抜き出してみたいと思います。
ちなみに得られるのは線形回帰ではなく、多数決で決まるプロットをできるだけ多く通った直線です。
目次
ランダムプロットを生成
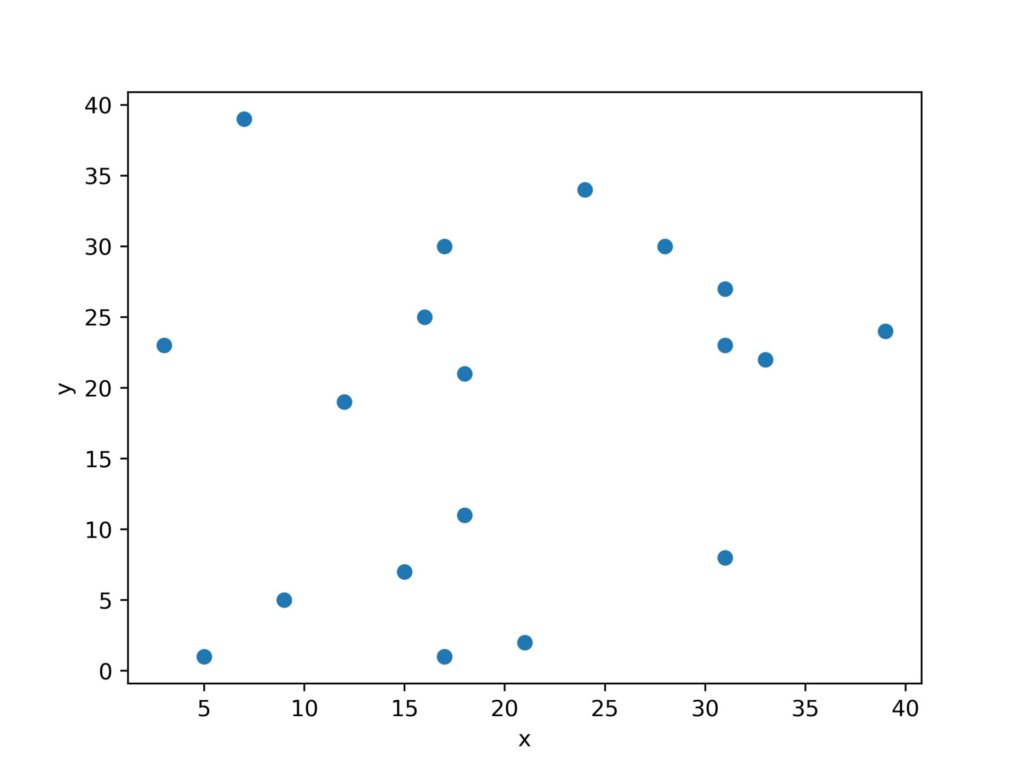
まずは直交座標上にランダムなプロットを20個生成します。
import numpy as np
import matplotlib.pyplot as plt
import math
import itertools
import random
import sympy as sym
from tqdm import tqdm
fig = plt.figure()
x = [random.randint(0,10) for i in range(20)]
y = [random.randint(0,40) for i in range(len(x))]
plt.scatter(x,y)
plt.xlabel('x')
plt.ylabel('y')
fig.savefig('img_random_xy.jpg',dpi = 500)以下の散布図が得られました。
ρ-θ空間への射影
上記のプロット全てを極座標変換してプロットしていきます。
fig = plt.figure()
ans_list = []
θ = sym.symbols('θ')
PI = np.pi
sin = sym.sin(θ)
cos = sym.cos(θ)
for i in range(len(x)):
θ = np.linspace(0,PI,1000)
ρ = x[i]*cos + y[i]*sin
plt.scatter(θ,x[i]*np.cos(θ) + y[i]*np.sin(θ),color = "black",s= 1)
for j in tqdm(range(len(x))):
if i!=j:
ans_j = sym.solve(ρ-(x[j]*cos + y[j]*sin))
if len(ans_j) == 1:
ans_list.append(ans_j[0])
max_overlapping =max([ans_list.count(i) for i in ans_list])
for i in ans_list:
if ans_list.count(i) == max_overlapping:
print(i)
plt.grid()
plt.xlabel('θ')
plt.ylabel('ρ')
fig.savefig('img_rth.jpg',dpi = 500)ついでに、一番多く交差する曲線の交点を求めておきました。
for i in [x[i]*np.cos(th) + y[i]*np.sin(th) for i in range(len(x))]:
print([x[i]*np.cos(th) + y[i]*np.sin(th) for i in range(len(x))].count(i))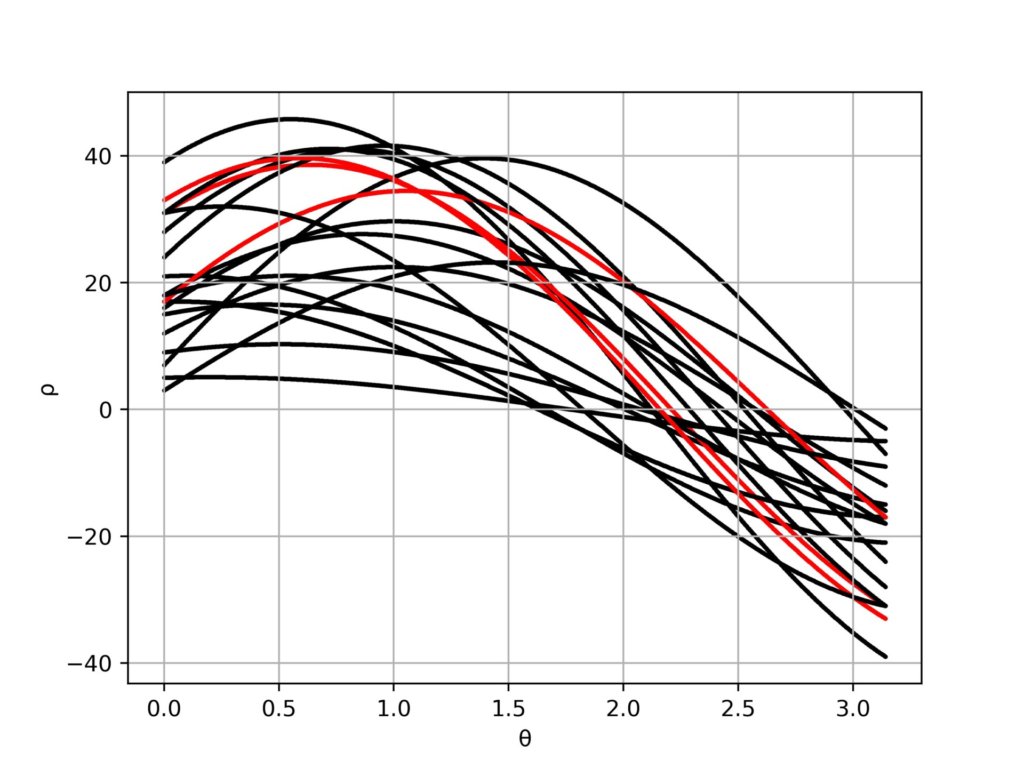
θ=arctan(2)
ρ=34.4この時、3つの曲線が交差するようです。意外と少ないですね。
2つのパラメータがわかったので後は直交座標系に戻すだけです。
以上のようにして、ランダムなプロットから直線を見つけ出すことができますが、線形回帰と違い画像中の直線を見つけるのに特化しているようです。



