局所最小値を求める
以下の関数について、エポック数100,学習レート0.01のパラメータを使用して、関数の局所最小値を求めてみます。
import numpy as np
import matplotlib.pyplot as plt
fig = plt.figure()
def ft(t:float)->float:
return 4*t**2 - 3*t + 2
def deriv(t:float)->float:
return 8*t - 3
t = np.linspace(-2,2,2001)
#Starting point
lc_min = np.random.choice(t,1)
# learning params
learning_rate = .01
epochs = 100
for i in range(epochs):
grad = deriv(lc_min)
lc_min-= learning_rate*grad
plt.plot(t,ft(t), t,deriv(t))
plt.plot(lc_min,deriv(lc_min),'ro')
plt.plot(lc_min,ft(lc_min),'ro')
plt.xlim(t[[0,-1]])
plt.grid()
plt.xlabel('t')
plt.ylabel('f(t)')
plt.legend(['f(t)','df','f(t) min'])
plt.title('Empirical local minimum: %s'%lc_min[0])
plt.show()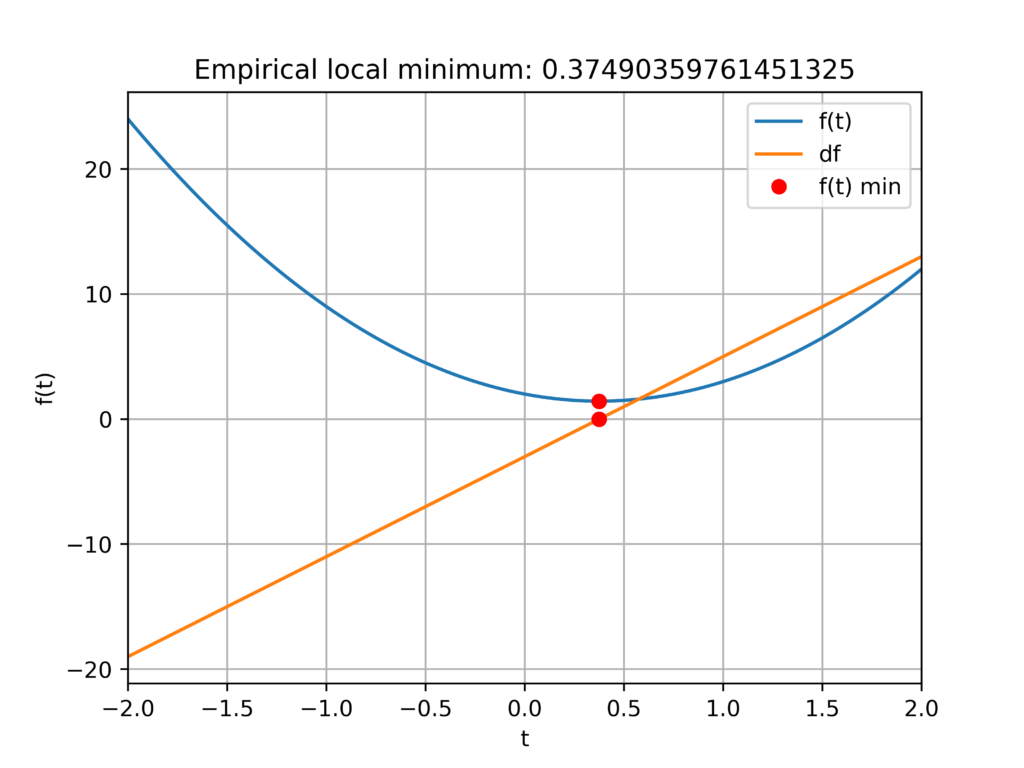
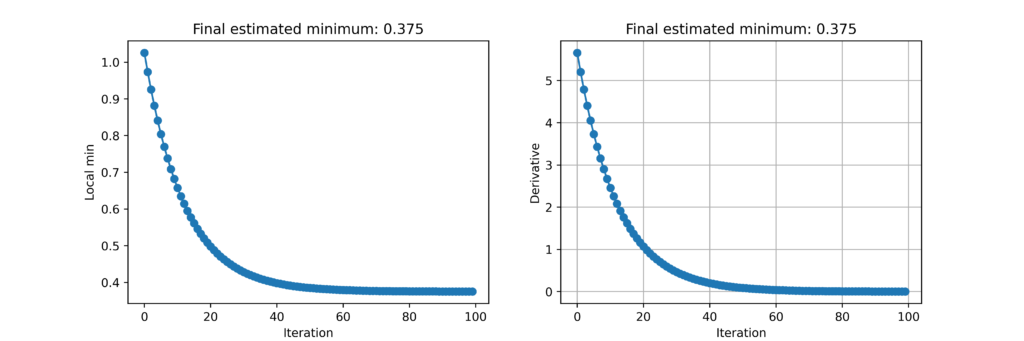
ここで、漸近していく様子を以下のように追跡すると、どのように収束していくかがわかります。
learning_rate = .01
epochs = 100
modelparams = np.zeros((epochs,2))
for i in range(epochs):
grad = deriv(lc_min)
lc_min-= learning_rate*grad
modelparams[i,0] = lc_min
modelparams[i,1] = grad
fig,ax = plt.subplots(1,2,figsize=(12,4))
for i in range(2):
ax[i].plot(modelparams[:,i],'o-')
ax[i].set_xlabel('Iteration')
ax[i].set_title(f'Final estimated minimum: {lc_min[0]:.3f}')
plt.grid()
ax[0].set_ylabel('Local min')
ax[1].set_ylabel('Derivative')
fig.savefig("a.png",dpi = 500)