酸素移動容量係数KLAの求め方

酸素の水に対する溶解度は約7.75 mg/L　(28℃)と、かなり小さいため、酸素を呼吸に使う微生物を培養する場合には培養液への通気を行う必要が出てきます。

その中で、通気の指標としてよく使われる酸素移動容量係数$K_L a$の導出を行なってみます。

ガルバニ電極による溶存酸素(DO)測定原理

作用電極をPt, 対極をPb, 電解液をKOHとし、作用電極と対極を接続すると、以下の酸化還元反応が起こります。

$\ce{O_2} + \ce{2H_2O}+4e^- \to \ce{4OH^-}$

$\ce{2Pb}\to \ce{2Pb^{2+}}+4e^-$

$\ce{2Pb^{2+}} + \ce{4OH^-}\to \ce{2Pb(OH)_2}$

$\ce{O_2} + \ce{Pb} + \ce{2H_2O}\to \ce{2Pb(OH)_2}$

この時、作用極(Pt)側にテフロン隔膜を挟んでおけば、電極を流れる電流は電解液（培養液）内の酸素分圧に比例することになります。

上記のOD測定を利用して、経時変化をトラッキングします。

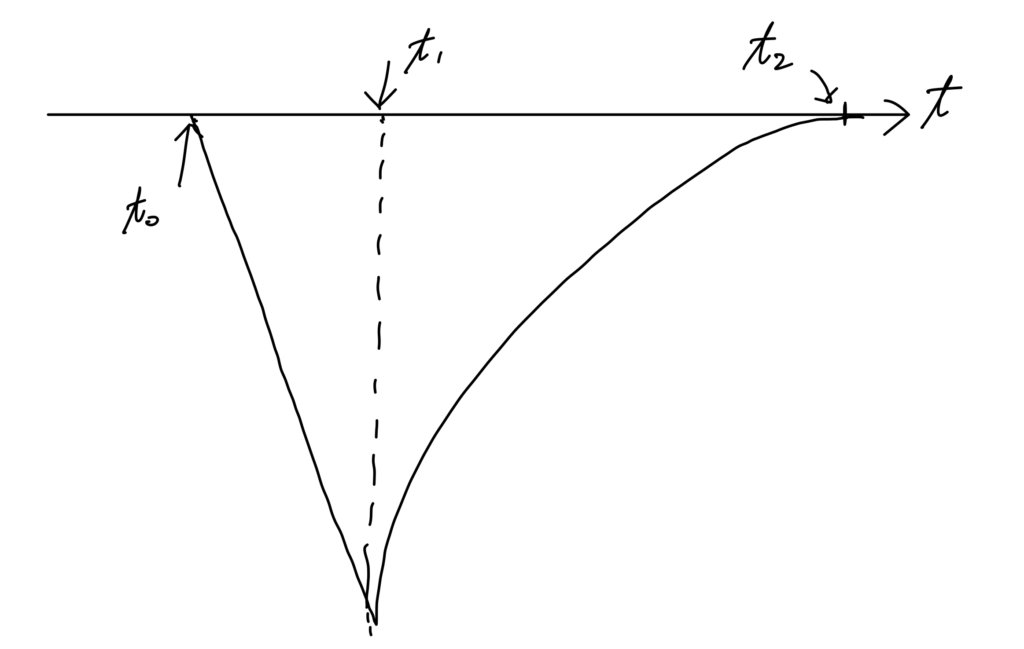
上記のグラフ(縦軸はOD)の$t_0$時点で通気を停止した後、$t_1$で通気を再開すると、$t_2$までの間、ODはカーブを描きながら定常値に戻っていきます。

上記の現象を定式化していきます。

DOに関して、

$$\frac{dC}{dt} = k_La(C^* – C)-Q_{\ce{O_2}}M$$

$C (mg/L)$:培養液のDO濃度

$C^* (mg/L)$:酸素消費がない場合の培養液のDO濃度

$M (g/L)$菌体濃度

$Q_{\ce{O_2}(mg_\ce{O_2}/g_{cell}/h)}$ 比呼吸速度

$ k_La(h^{-1})$酸素移動容量係数

ここで、定常状態について考えると、この時のDO濃度を$\bar{C}$として、以下のように表すことができる。

$$\bar{C} = C^* -\frac{Q_{O_2}M}{k_La}$$

よって、

$$\frac{dC}{dt} = -k_La(C-\bar{C})$$

上記の微分方程式から、

$$C(t) = \bar{C}+(C_0-\bar{C})e^{-k_Lat}$$

を得ます。

上記の式から、時刻tにおけるDO濃度を求めることができるようになりました。

少し式を変形すると、

$$ \bar{C}-C(t) = (\bar{C}-C_0)e^{-k_Lat}$$

ここで、時刻tの時の$ \bar{C}-C(t)$が$\frac{ \bar{C}-C(t)}{e}$となるまでの時間を$\tau (h)$とすると、

$$\ln(\frac{1}{e}) = -k_La\tau = -1$$

となり、結果的に$\frac{1}{\tau}$を求めれば良いことになります。