発癌リスク評価とポアソン分布(遺伝子ヒットモデル）

ポアソン分布

ポアソン分布とは、一定時間内にランダムなイベントが何回発生するかを表す分布です。

一般に、単位時間あたり平均$\lambda$回起こるランダムな事象が、単位時間に$k$回起こる確率$P(k)$は以下のように与えられます。(時間軸が固定されることを想定。）

$$P(k) = e^{-\lambda}\frac{\lambda ^ k}{k!}$$

pythonで描画

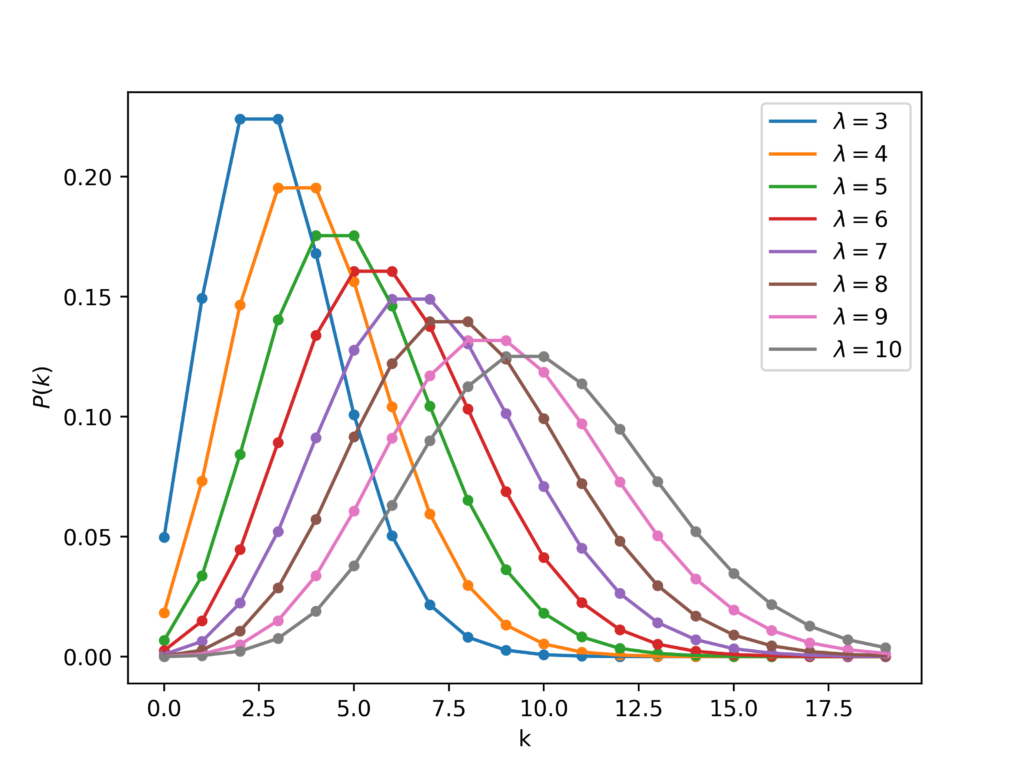
単位時間$t$に平均$l$回起こるランダムな事象が、時間$t$の中で$k$回起こる確率を可視化してみます。

import numpy as np 
import matplotlib.pyplot as plt

fig = plt.figure()


def poisson(k:int,l:int) -> float:
    k_f = 1
    for i in range(1,k+1):
        k_f*=i 
    return np.exp(-l)*l**k/k_f

x = [i for i in range(0,20)]
for l in range(3,11):
    y_l = [poisson(k,l) for k in x]
    plt.plot(x,y_l)
    plt.scatter(x,y_l,s=15)

plt.xlabel("k")
plt.ylabel(r"$P(k)$")

fig.savefig("a.png",dpi=500)

実行結果

ツーヒットモデル

発癌のリスクを評価するツーヒットモデルでは、化学物質が遺伝子に2回以上ヒットすると細胞が癌化します。化学物質が遺伝子にヒットする確率を、確率係数$q(kg\:d/ mg)$,暴露量$D(mg/kg/d)$の元で$\lambda = qD$とすると、2回ヒットした場合の発癌の確率は以下のポアソン分布を用いて、

$$h(k)=e^{-\lambda}\frac{\lambda ^k}{k!}$$

$$\begin{align}P(D)&=\sum_{i=2}^\infty h(i)\\&=1-h(1)-h(0)\\&=1-e^{-qD}(1+qD)\end{align}$$

と表されます。発癌の確率を極めて低いものとみなせば、

$$e^{-qD}≈ 1 – qD + \frac{q^2 D^2}{2} + … \simeq 1-qD$$

より、$P(D)=(qD)^2$