一般的に制限酵素の切断領域は回文構造(パリンドローム)になっています。
今回はその回文領域を求めるためのアルゴリズムについて考えていきます。
目次
アルゴリズム
切断領域の定義を4-12のヌクレオチドから構成される回文領域とします。
相補鎖および逆相補鎖の生成
初めに、対象配列の相補鎖および逆相補鎖を用意しておきます。
逆相補鎖は回文構造の探索用、相補鎖は回文の検証に使用します。
from Bio.Seq import Seq
seq = Seq('''GCGCTATAGTCCCCTCCAGTCCCAAACTCGAGGTAGGAGGGTGTGCTAGATTTTGTTTTA
GAAGTAAAGGTCTCGTCGGCAGCTTGTTTGGAGAGCTCCGCTAAATAAGAATCCACTTAA
CAAAGACGCCACACACAAGTACCTCGTACGTAGAAGCACTGCGGAAATACTAAGCTCCAA
TCGCGTTTGAGCAGTCCTCTTCACTGACTAGTTTTCCAGACGGGCCTAGCGCCGCGGCAA
GCCGGTACTATGTGATCACCCCGGTAAGGTGGGCCTTTGCAGGCCAGCATTCGCTCAAGA
ACCGCATCAACGCCTGCACTGCCGTTGAGATTGGATTTCGGATGATCGACGCGAGTATAG
TATCGTATCGTAGGCTGAAGTATCGAGCCATTGAGCTCGAAAGGAGTAACTATATCCCTA
ATGCCCACTAGGCTTAGTTAAAGGACGTCCTTGCGAGGACCTGAGGTGGATGGCATTCTT
TCATGCACACGGTCGGTACACGTTGCTTTGGCCCGCTGAGGTAGCATTATATTGTCCTGG
CAAACGAAGGCACCGTTCATTCTGGTTATCGGACATTATTGCTGTGTCTCCATTTAGCTG
GGATGGAGATCTCACGGAATTACGCCGAACTCTGTTTAAGAAACCACTTATCCTCTATGG
GAATCTCTCGTTTGTCTTGCGCTCCAGCCCGTGGCTGTTAATTGTAGCCGTGCTACGGTA
TCAATTCTCACTGATACCTTCAAGGCGTATACTGGCTAGTGGAAATGGTCGGGCGGTGCC
CATGCTCAATACTTTTCACTTTAGCATATCTATTCTCGAGATATCCGCAACAGCAAACAG
CAACGCGTGCTAAGGCATGTTGATAATGTATAGGGCGGTCGTGCCATGCGCG'''.replace('\n',''))BiopythonライブラリのSeqモジュールを使用して瞬時に変換します。
seq_c = seq.complement()
seq_r = seq.reverse_complement()回文構造の探索
次に、逆相補鎖を利用して、条件を満たすパリンドロームの候補となる配列を探索していきます。
この時、候補となる配列の長さが偶数であることに注意します。
s_l= []
for i in range(len(seq)):
s_i = seq_r[i:]
if len(s_i) >= 12:
for j in range(4,13):
s = s_i[:j]
if s in seq and s not in s_l and len(s)%2 ==0 :
s_l.append(s)
elif len(s_i) < 12:
for j in range(4,len(s_i)+1):
s = s_i[:j]
if s in seq and s not in s_l and len(s)%2 ==0 :
s_l.append(s)探索結果をs_lに代入しました。
回文配列の検証
通常ならs_l中に入っているもののインデックスを片っぱしからfindメソッドで取り出していけばいいのですが、findメソッド及びindexメソッドには最初にマッチしたものを取り出したら仕事を辞めてしまうという欠点があります。
そのため、s_l中の全ての断片が必ずしも回文となると言うことはできません。
そこで、以下のように回文の検証を行ったものを[開始地点,長さ]と言う形で取り出してみたいと思います。
t_l = [[t+1,len(s)] for s in s_l for t in range(len(seq)) if seq[t:t+len(s)] == s and seq_c[t:t+len(s)] == s[::-1]]結果
回文配列の結果をターミナルに出力します。
for i in sorted(t_l):
print(str(i[0])+' '+str(i[1]))実行結果
1 4
4 6
5 4
27 6
28 4
46 4
81 4
93 6
94 4
117 4
139 4
145 6
146 4
147 6
148 4
173 4
182 4
207 6
208 4
223 4
226 4
229 4
231 8
232 6
233 4
242 4
245 4
252 8
253 6
254 4
261 4
272 4
278 4
282 4
315 4
344 4
346 4
350 4
356 4
383 4
393 6
394 4
397 4
411 4
412 4
428 4
438 4
441 12
442 10
443 8
444 6
445 4
482 4
484 4
496 4
500 4
510 4
528 4
529 4
596 4
606 8
607 6
608 4
618 4
636 4
679 4
698 4
700 4
723 4
747 6
748 4
756 4
781 4
806 4
814 8
815 6
816 4
820 6
821 4
843 6
844 4
856 4
869 4
885 4
888 4
889 4意外と多いですね。
計算量
見ての通り、二重ループを使用しているため計算量はO(N^2)となることは確実ですが、上記の処理を関数化して文字列数による実行時間の推移をグラフにしてみます。
from Bio.Seq import Seq
import time
def get_locations_of_restriction_sites(seq):
seq = Seq(seq.replace('\n',''))
seq_c = seq.complement()
seq_r = seq.reverse_complement()
s_l= []
for i in range(len(seq)):
s_i = seq_r[i:]
if len(s_i) >= 12:
for j in range(4,13):
s = s_i[:j]
if s in seq and s not in s_l and len(s)%2 ==0 :
s_l.append(s)
elif len(s_i) < 12:
for j in range(4,len(s_i)+1):
s = s_i[:j]
if s in seq and s not in s_l and len(s)%2 ==0 :
s_l.append(s)
return sorted([[t+1,len(s)] for s in s_l for t in range(len(seq)) if seq[t:t+len(s)] == s and seq_c[t:t+len(s)] == s[::-1]])意外とコンパクトにまとまりました。
ここから、推移を確認するためにランダムに塩基配列を増やしていきながら経過を見ていきます。
import random
from matplotlib import pyplot as plt
from tqdm import tqdm
if __name__ == '__main__':
fig = plt.figure()
plt.grid()
plt.xlabel('bp')
plt.ylabel('time(s)')
nucleotides = ['A','C','G','T']
seq = ''
k = 10
for i in tqdm(range(100)):
s = time.time()
seq += ''.join(random.choices(nucleotides,k=k))
get_locations_of_restriction_sites(seq)
plt.scatter(k*i,time.time()-s,c='blue')
fig.savefig('a.jpg')出来上がった画像がこちらです。
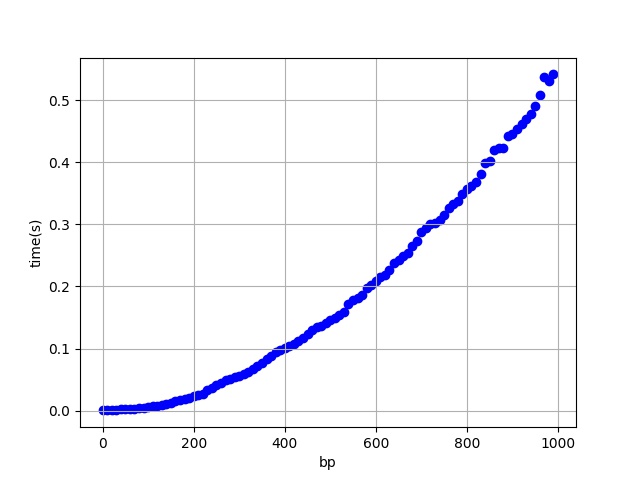
ちゃんと二乗時間になってますね。
次はどうにかして線形時間に落とせるアルゴリズムを考えてみたいと思います。



