本記事では、経路にバリアフリー対応かどうかの情報を持たせた隣接行列を作成し、バリアフリーかつ最短である経路をDijkstra法を用いて探索します。
目次
Pythonモジュール
以下モジュールを使用します。
import random
import numpy as np
import matplotlib.pyplot as plt
import networkx as n
from graphviz import Graph経路情報の生成
今回は経路情報を隣接行列によって表現します。
例えば、A->Bという建物の移動に5分かかる場合、G[0][1] = 5 というように隣接行列を生成します。
今回はランダムシード値を固定して経路情報を生成します。
この時、隣接行列の各要素を整数ではなく、以下のようなクラスのオブジェクトとして保持させることでバリアフリー経路情報ラベルを付与します。
class AdjNode:
def __init__(self, weight: int, is_Barrier_free: bool) -> None:
self.weight: int = weight
self.is_Barrier_free: bool = is_Barrier_free
def __add__(self, other):
return self.weight + other.weight
def __repr__(self) -> str:
return f"{self.weight*1 if self.is_Barrier_free else self.weight*-1}"隣接行列を生成して可視化します。
def transpose(G:list]) -> list]:
rows = len(G)
cols = len(G[0])
G_T = [[None for _ in range(rows)] for _ in range(cols)]
for i in range(rows):
for j in range(cols):
G_T[j][i] = G[i][j]
return G_T
def add_matrices(G, T):
rows = len(G)
cols = len(G[0])
result = [[None for _ in range(cols)] for _ in range(rows)]
for i in range(rows):
for j in range(cols):
if G[i][j].weight != 0:
result[i][j] = G[i][j]
elif T[i][j].weight != 0:
result[i][j] = T[i][j]
else:
result[i][j] = G[i][j]
return result
def generate_random_G(R:int) -> np.ndarray:
random.seed(10)
weights_cs = [0]*50 + [1]*4 + [2]*2 + [3]*2 + [3]*6 + [4]*3 + [5]*6
p = [-1]*5 + [1]*21
def get_weight():
return random.choice(weights_cs) * random.choice(p)
G : list[AdjNode] = [[AdjNode(0,False) for i in range(R)] for j in range(R)]
for i in range(R):
for j in range(R):
if i == j or i < j:
continue
w = get_weight()
G[i][j].weight = abs(w)
G[i][j].is_Barrier_free = True if w > 0 else False
return G
G = generate_random_G(15)
GraphvizObject = Graph(format="png")
GraphvizObject.attr("node", shape="circle")
G : list[AdjNode] = add_matrices(G, transpose(G))
nodes, path_weights = [str(chr(i).upper()) for i in range(97,len(G)+97)], {}
for i in range(len(G)):
for j in range(len(G[0])):
if G[i][j].weight != 0:
path_weights[f"{nodes[i]}->{nodes[j]}"] = G[i][j]
if i>j:
print(type(G[i][j]))
GraphvizObject.edge(str(nodes[i]),str(nodes[j]),label=str(G[i][j].weight),color='black' if G[i][j].is_Barrier_free else 'red')
GraphvizObject.render("G")実行結果
赤色がバリアフリー非対応の経路、つまり探索時に避けるべき経路となります。
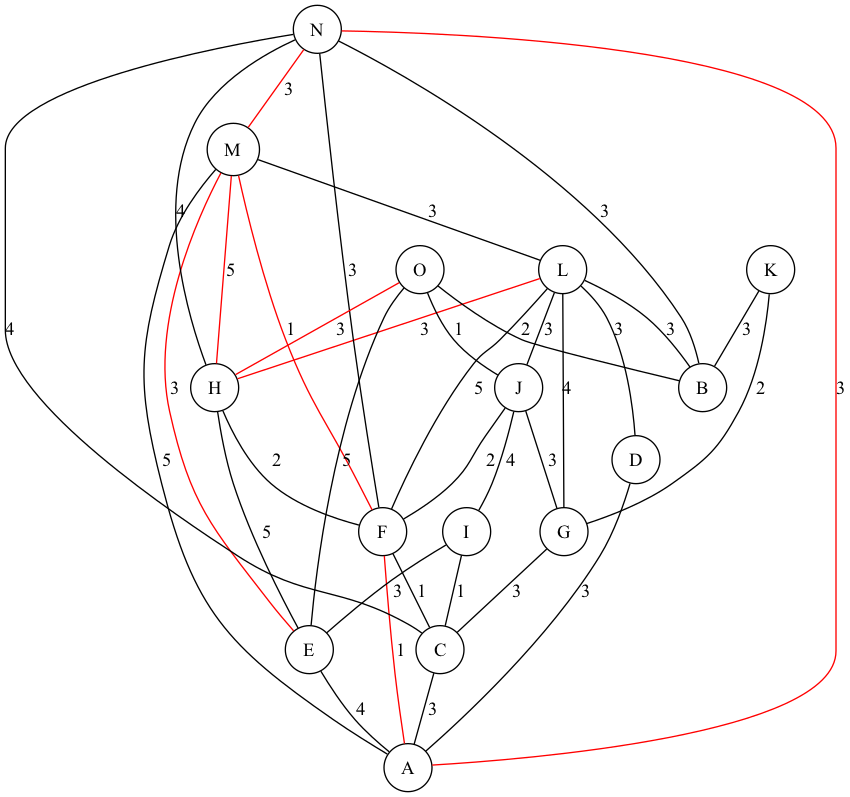
探索アルゴリズム
queueを使用したバックトラックによるDijkstraアルゴリズムを実装します。
class Node:
def __init__(self,name:str) -> None:
self.name:str = name
self.adj:dict[str,int] = {}
self.d:float = float('inf')
self.explored:bool = False
self.prevNode:Node | None = None
def __repr__(self) -> str:
return self.name
def set_explored(self,e:bool) -> None:
self.explored = e
def set_d(self,d:int) -> None:
self.d = d
class PathFinder:
def __init__(self,all_paths:dict[str,int],nodes_string:list[str]) -> None:
self.nodes_string: list[str] = nodes_string
self.nodes:dict[str,Node] = {i:Node(i) for i in nodes_string}
for i in all_paths.keys():
self.nodes[i[0]].adj[i[3]] = all_paths[i]
def search_path(self,startNode:str,endNode:str):
#最短距離を無限大に初期化
for i in self.nodes.keys():
self.nodes[i].d = float('inf')
queue:list[str] = [startNode]
#currNodeを初期化
currNode: str = queue[0]
#currNodeの距離を初期化
self.nodes[currNode].set_d(0)
#初期ノードのprevNodeを初期化
self.nodes[currNode].prevNode = None
while len(queue) >0:
currNode = queue.pop(0)
adjs = self.nodes[currNode].adj
for i in adjs.keys():
tmp_d:float = self.nodes[currNode].d + self.nodes[currNode].adj[i]
if self.nodes[i].d > tmp_d:
#スタートノードからの最短到達距離を更新
self.nodes[i].set_d(int(tmp_d))
self.nodes[i].prevNode = self.nodes[currNode]
self.nodes[i].set_explored(True)
queue.append(i)
cNode:Node = self.nodes[endNode]
#Backtrack
s:list[str] = [endNode]
while cNode.prevNode != None:
cNode = cNode.prevNode
s.append(cNode.name)
return [s[::-1],self.nodes[endNode].d]バリアフリー経路の探索開始
上記アルゴリズムで、バリアフリー経路を迂回して経路探索を行います。
path_weights = {i: path_weights[i].weight for i in path_weights.keys() if path_weights[i].is_Barrier_free}
print(path_weights)
W = PathFinder(path_weights,nodes)
print(W.search_path("A","B"))
print(W.search_path("A","C"))
print(W.search_path("A","D"))
print(W.search_path("A","E"))
print(W.search_path("A","F"))
print(W.search_path("A","G"))
>>>
[['A', 'D', 'L', 'B'], 9]
[['A', 'C'], 3]
[['A', 'D'], 3]
[['A', 'E'], 4]
[['A', 'C', 'F'], 4]
[['A', 'C', 'G'], 6]AからBまでの最短距離をバリアフリー無効な経路を迂回して探索できていることがわかります。



