レーベンバーグ・マルカート法を内部実装で用いているScipyのCurv_fit関数を使用して、非線形での最小二乗法によるパラメータ決定を行います。
今回は以下の単純なミカエリス・メンテン酵素反応速度式を用いて検証を行います。
$v = \frac{V_{max}[S]}{K_M+[S]}$
ここで、決定すべきパラメータを以下のように定義します。
$V_{max} = \beta_1, \:\:K_M = \beta_2$
目次
データ
wikiぺディアのガウスニュートン法のページから拾ってきました。
v = np.array([0.05,0.127,0.094,0.2122,0.2729,0.2665,0.2217])
s = np.array([0.038,0.194,0.425,0.626,1.253,2.500,3.740])実装
import numpy as np
from scipy.optimize import curve_fit
import matplotlib.pyplot as plt
fig = plt.figure()
v = np.array([0.05,0.127,0.094,0.2122,0.2729,0.2665,0.2217])
s = np.array([0.038,0.194,0.425,0.626,1.253,2.500,3.740])
#関数の定義
def f(s,beta_1,beta_2):
return beta_1*s/(beta_2+s)
#パラメータの初期化
init_beta = [1.0, 1.0]
params, covariance = curve_fit(f, s, v, p0=init_beta, method='lm')
s_theta = np.linspace(min(s),max(s),100)
theta = [f(i,params[0],params[1]) for i in s_theta]
plt.plot(s_theta,theta,color = "red")
plt.scatter(s,v,s=10,color = "black")
plt.grid()
plt.xlabel("[S]")
plt.ylabel("v")
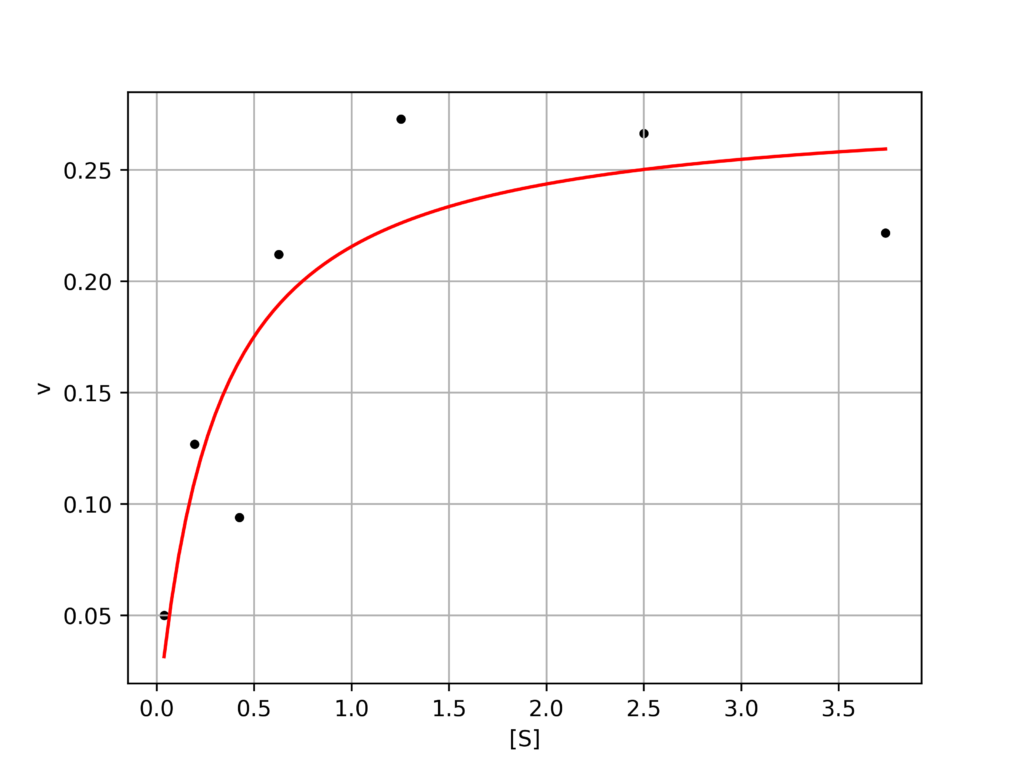
fig.savefig("result.png",dpi = 500)実行結果