次元削減アルゴリズムはPCAやt-SNEなどがありますが、その中の一つSVDについて見ていきます。
目次
特異値の定義
$$\mathbf{A}\in\mathbb{R}^{m\times n},\:\:\mathbf{v}\in\mathbb{R}^n,\:\mathbf{u}\in\mathbb{R}^m$$
について、以下二つの方程式が成り立つとします。
$$\mathbf{A}\mathbf{v}=\sigma\mathbf{u}$$
$$\mathbf{A}^\mathrm{T}\mathbf{u}=\sigma\mathbf{v}$$
この時、
$$\mathbf{A}^\mathrm{T}\mathbf{A}\mathbf{v}=\sigma^2\mathbf{I}\mathbf{v}$$
より、以下のように固有値分解と同様の固有方程式に持っていきます。
$$|\mathbf{A}^\mathrm{T}\mathbf{A}-\sigma^2\mathbf{I}|=0$$
または、
$$|\mathbf{A}\mathbf{A}^\mathrm{T}-\sigma^2\mathbf{I}|=0$$
より、
$$\det (\mathbf{B}-\lambda\mathbf{I})=0$$
よって、上記の固有方程式から求めた固有値の平方根が特異値となります。
特異値分解
特異値分解は以下のように与えられます。
$$\mathbf{A}=\mathbf{U}\mathbf{\Sigma}\mathbf{V}^\mathrm{T}$$
この時、$\mathbf{U}$は左特異ベクトル、$\mathbf{V}$は右特異ベクトルと呼ばれます。
特異値分解の求めかた
上式の両辺に右から$\mathbf{A}^\mathrm{T}$をかけます。
$\mathbf{A}\mathbf{A}^\mathrm{T}=\mathbf{U}\mathbf{\Sigma}\mathbf{V}^\mathrm{T}\mathbf{V}\mathbf{\Sigma}^\mathrm{T}\mathbf{U}^\mathrm{T}$
特異ベクトルは両方直交行列なので、
$\mathbf{A}\mathbf{A}^\mathrm{T}=\mathbf{U}\mathbf{\Sigma}\mathbf{\Sigma}^\mathrm{T}\mathbf{U}^\mathrm{T}$
固有方程式で対角化を行います。
$$\det(\mathbf{A}\mathbf{A}^\mathrm{T}\mathbf{I}-\lambda\mathbf{I})=0$$
ここで求めた固有値を並べたものが左特異ベクトルとなります。
右特異ベクトルに対しても同様の操作を行います。
この時、各ベクトルはノルムを1に正規化しておきます。
ここで、
$\mathbf{\Sigma}\mathbf{\Sigma}^\mathrm{T}$は$\mathbf{A}\mathbf{A}^\mathrm{T}$の固有値を並べた対角行列となります。
以下pythonで特異値分解を行ってみます。
import numpy as np
from numpy.linalg import svd
A = np.array([[9, 2,5],[1,3,1]])
U, S, V_T = svd(A)
print("左特異値ベクトル行列")
print(U)
print("Σ")
print(np.diag(S))
print("右特異値ベクトル行列")
print(V_T)
#再構築
S_extended = np.zeros((U.shape[1], V_T.shape[0]))
np.fill_diagonal(S_extended, S)
reconstructed_A = np.dot(U, np.dot(S_extended, V_T))
U, S_extended, V_T, reconstructed_A
print(reconstructed_A)
>>>
[[-0.98162602 -0.19081498]
[-0.19081498 0.98162602]]
Σ
[[10.67181956 0. ]
[ 0. 2.66688345]]
右特異値ベクトル行列
[[-0.8457273 -0.23760681 -0.47779529]
[-0.27586837 0.96113991 0.01033083]
[-0.45677344 -0.14054567 0.87841046]]
[[9. 2. 5.]
[1. 3. 1.]]次元削減
上記の特異値分解を用いてデータの次元削減を行ってみます。
まずはデータを定義します。
今回は以下のように5次元のベクトルを薬剤処理群、非処理群それぞれ10ずつ用意します。
import random
random.seed(0)
data1 = [[0.99652549, -0.00581268, -0.01632635, -0.01567768, -0.01179158],
[1.01301428, 0.00895260, 0.01374964, -0.01332212, -0.01968625],
[0.99339944, 0.00175819, 0.00498690, 0.01047972, 0.00284280],
[1.01742669, -0.00222606, -0.00913079, -0.01681218, -0.00888971],
[1.00242118, -0.00888720, 0.00936742, 0.01412328, -0.02369587],
[1.00864052, -0.02239604, 0.00401499, 0.01224871, 0.00064856],
[0.98720311, -0.00585431, -0.00261645, -0.00182245, -0.00202897],
[0.99890117, 0.00213480, -0.01208574, -0.00242020, 0.01518261],
[0.99615355, -0.00443836, 0.01078197, -0.02559185, 0.01181379],
[0.99368096, 0.00163929, 0.00096321, 0.00942468, -0.00267595]]
data2 =[[-0.00678026, 1.01297846, -0.02364174, 0.00020334, -0.01347925],
[-0.00761573, 1.02011257, -0.00044595, 0.00195070, -0.01781563],
[-0.00729045, 1.00196557, 0.00354758, 0.00616887, 0.00008628],
[0.00527004, 1.00453782, -0.01829740, 0.00037006, 0.00767902],
[0.00589880, 0.99636141, -0.00805627, -0.01118312, -0.00131054],
[0.01133080, 0.98048196, -0.00659892, -0.01139802, 0.00784958],
[-0.00554310, 0.99529362, -0.00216950, 0.00445393, -0.00392389],
[-0.03046143, 1.00543312, 0.00439043, -0.00219541, -0.01084037],
[0.00351780, 1.00379236, -0.00470033, -0.00216731, -0.00930157],
[-0.00178589, 0.98449571, 0.00417319, -0.00944368, 0.00238103]]
data1 = [[i + random.random()/2 for i in j ] for j in data1]
data2 = [[i + random.random()/2 for i in j ] for j in data2]上記のデータを特異値分解します。
A = np.concatenate([data1,data2],axis=0)
U, S, V_T = svd(A)
print("左特異値ベクトル行列")
print(U)
print("Σ")
print(np.diag(S))
print("右特異値ベクトル行列")
print(V_T)
A = np.concatenate([data1, data2], axis=0)
# Performing Singular Value Decomposition (SVD)
U, S, V_T = svd(A)
>>>
S:[5.48177723 3.02584534 0.74248201 0.49349568 0.3683004 ]次元ごとの特異値を可視化してみます。
fig = plt.figure(figsize=(6,6))
sns.set()
plt.plot([i for i in range(1,6)],S,color = "blue",linewidth=1,marker="o")
plt.xlabel("Dimention(-)")
plt.ylabel("Singular value(-)")
plt.savefig("s_roll.png",dpi = 500)実行結果
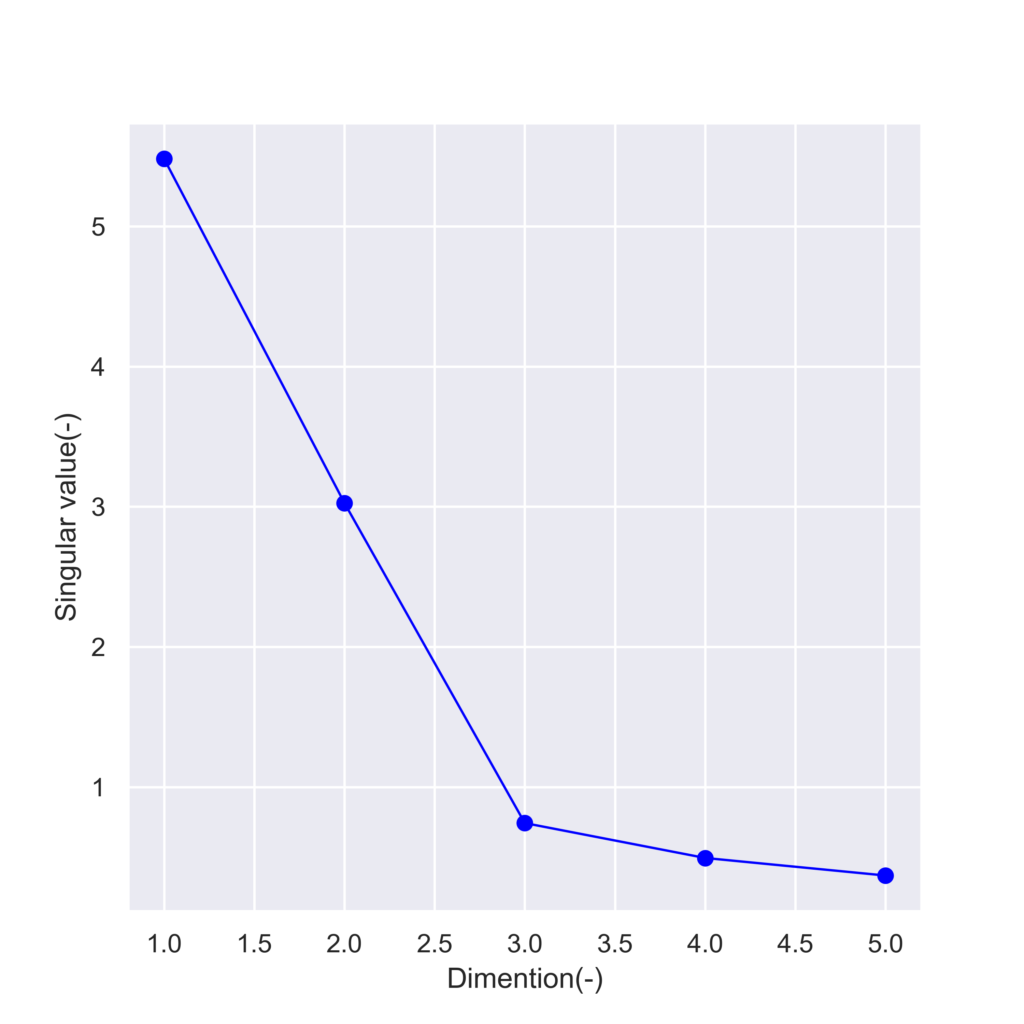
3次元までの寄与率が9割を超えているので、3次元空間にデータを射影してみます。
reduced_data = np.dot(A, V_T.T[:, :3])
# Separating the projected data for the two original datasets
reduced_data1 = reduced_data[:len(data1)]
reduced_data2 = reduced_data[len(data1):]
import seaborn as sns
sns.set()
# Plotting the results
plt.figure(figsize=(8, 8))
ax = plt.axes(projection='3d')
ax.view_init(elev=20, azim=20)
ax.scatter3D(reduced_data1[:, 0], reduced_data1[:, 1], reduced_data1[:, 2], color='blue', label='Negative Ctrl.',alpha=0.6)
ax.scatter3D(reduced_data2[:, 0], reduced_data2[:, 1], reduced_data2[:, 2], color='red', label='Positive Ctrl.',alpha=0.6)
plt.title('3D Projection using SVD')
plt.xlabel(f'Component 1 s = {round(S[0],1)}')
plt.ylabel(f'Component 2 s = {round(S[1],1)} ')
plt.legend()
plt.savefig("result_3D.png",dpi = 500)実行結果
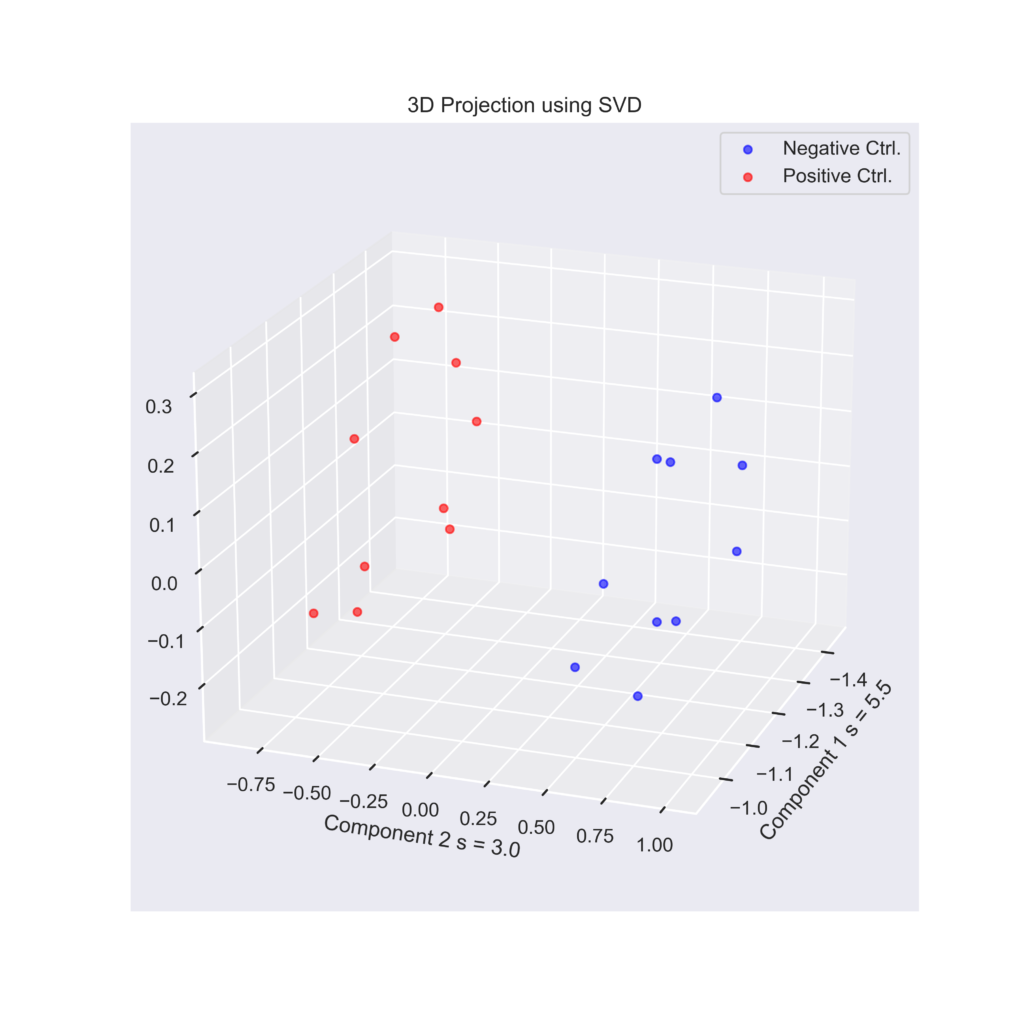
それぞれの薬剤処理群に属するデータポイントがうまく切り離されていることがわかります。



