ここでは対数増殖期の各タイムポイントにおける細胞の濃度(OD600)を利用して、細胞の比増殖速度を求めます。
目次
比増殖速度の定義
比増殖速度は、1つの細胞が単位時間あたりにどれだけ分裂するかを表す係数です。
一定条件のもとで、初発細胞量をX(g)、比増殖速度をμ(1/h),時間をt(h)とすると、
$$\frac{dX}{dt} = \mu X$$
上記の微分方程式を解くと、初発細胞量をX0(g)として、
$$\ln \frac{X}{X_0}=\mu t$$
を得ます。
ここで、細胞の倍加時間は
$$t_d = \frac{\ln 2}{\mu}$$
となります。
最小二乗法による増殖曲線のフィッティング
対数増殖期のデータを使用するため、フィッティングに使用する方程式を以下のように定義します。
$$y = ae^{\mu t}+c$$
指数部分にパラメータがあるので、式を線形にするために対数をとって展開します。
$$\ln y = \ln(ae^{\mu t}+b) $$
正規方程式を作成できるように式を変形します。
$$\ln y = \mu t+\theta$$
ここで、
$$ \mathbf{f} = \begin{pmatrix} \ln y_1 &\cdots &\ln y_n \end{pmatrix}\in\mathbb{R}^n$$
$$\mathbf{W} = \begin{pmatrix} t_1&1&1\\\vdots&\vdots&\vdots \\ t_n&1&1\end{pmatrix}$$
とすると、
$$\begin{pmatrix} \mu & \theta \end{pmatrix} = (\mathbf{W}^\mathrm{T}\mathbf{W})^{-1}\mathbf{W}^\mathrm{T}\mathbf{f}\in \mathbb{R}^2$$
よって、上記の式によって非増殖速度を求めることができます。
Pythonで実装
以下のデータを使用します。
OD600 = [0.0038999969999999884, 0.003599999999999992, 0.0033999959999999885, 0.003700001999999994, 0.0038999969999999884, 0.00399999899999999, 0.004100000999999992, 0.004100000999999992, 0.00449999999999999, 0.004600001999999992, 0.004899998999999988, 0.004600001999999992, 0.005199996999999998, 0.005400000999999988, 0.00600000299999999, 0.0064000029999999875, 0.006999997999999993, 0.006699999999999998, 0.006900003999999987, 0.00879999799999999, 0.00929999899999999, 0.009599996999999985, 0.011099999999999985, 0.011899998999999994, 0.013599997999999988, 0.015100000999999988, 0.017199998999999994, 0.01950000099999999, 0.022300002999999985, 0.02490000299999999, 0.028900002999999994, 0.03299999799999999, 0.037900007, 0.04230000699999999, 0.048500007, 0.054799995000000004, 0.06379999799999998, 0.071699998, 0.081000006, 0.093300006, 0.10669999399999998, 0.11999999599999998, 0.134299999, 0.150500005, 0.16929999599999995, 0.18120000399999997, 0.19319999799999998, 0.20989999799999998, 0.23080000899999997, 0.25169999, 0.27089998699999995, 0.293800002, 0.31459999699999996, 0.32879999899999995, 0.343800014, 0.359900004, 0.373200005, 0.388899988, 0.40390000299999995, 0.416699982, 0.427700019, 0.439399993, 0.45070002099999995, 0.46280000199999993, 0.47580001399999994, 0.49029997599999997, 0.5005, 0.5136000279999999, 0.523699975, 0.536100006, 0.54660002, 0.558700001, 0.5671000239999999, 0.579200006, 0.590199983, 0.601100004, 0.60940001, 0.620399988, 0.6292999739999999, 0.639499998, 0.652900016, 0.658899999, 0.668300009, 0.680500007, 0.690499997, 0.69740001, 0.7029999849999999, 0.710899985, 0.719400024, 0.7255000229999999, 0.731399989, 0.7392999889999999, 0.749900019, 0.753400004, 0.760399973, 0.766800022, 0.772699988, 0.778900003, 0.7829000119999999, 0.785000002, 0.792900002, 0.798400021, 0.803499973, 0.806799984, 0.814600027, 0.815900004, 0.818999982, 0.8232999799999999, 0.826400018, 0.833200014, 0.838799989, 0.843700027, 0.846299982, 0.853499985, 0.853600001, 0.857600009, 0.8595000269999999, 0.860399997, 0.863300002, 0.861500001, 0.863000011, 0.867099977, 0.8657999989999999, 0.864800012, 0.8675999999999999, 0.864900029, 0.8651000019999999, 0.864100015, 0.864699996, 0.863000011, 0.861600018, 0.862799978, 0.8606999869999999, 0.859299994, 0.8610999939999999, 0.856500006, 0.857200003, 0.8559999819999999, 0.854599988, 0.853300011, 0.852399981, 0.8512999769999999, 0.850699997, 0.854199982, 0.8584999799999999, 0.863400018, 0.865699983, 0.8664999959999999, 0.865299976, 0.8624999879999999, 0.864699996, 0.862700021, 0.862199998, 0.8609999779999999, 0.857200003, 0.856900012, 0.857499993, 0.856699979, 0.852699971, 0.850400007, 0.85059998, 0.847399986, 0.8436000109999999, 0.844700015, 0.844700015, 0.842600024, 0.838799989, 0.8407000059999999, 0.837299979, 0.835899985, 0.838200009, 0.834399974, 0.833900011, 0.8330999969999999, 0.8324, 0.831700003, 0.830000019, 0.831100023, 0.827699995, 0.828999972, 0.828500009, 0.8272999879999999, 0.827199972, 0.8265999909999999, 0.827400005, 0.828100002, 0.824399984, 0.823500013, 0.823100007, 0.819200015, 0.8174999709999999, 0.816400027, 0.8138000129999999, 0.8138000129999999, 0.8105000019999999, 0.810699975, 0.807700014, 0.8050999999999999, 0.803599989, 0.801900005, 0.803000009, 0.799500024, 0.79660002, 0.798800027, 0.798400021, 0.794700003, 0.7927999849999999, 0.790699995, 0.7905000209999999, 0.7894999739999999, 0.7916000249999999, 0.790699995, 0.790100014, 0.7866000289999999, 0.786999977, 0.783799982, 0.785000002, 0.783600008, 0.7825000049999999, 0.781500018, 0.7786000129999999, 0.777699983, 0.776199973, 0.776599979, 0.771500027, 0.770899987, 0.7690999869999999, 0.766100025, 0.766100025, 0.761199987, 0.759799993, 0.7585000159999999, 0.757400012, 0.758200026, 0.752499974, 0.752499974, 0.75109998, 0.7488000149999999, 0.75170002, 0.749900019, 0.746200001, 0.747800028, 0.745399988, 0.745399988, 0.744599974, 0.74380002, 0.740699983, 0.741799986, 0.743400013, 0.741200006, 0.742499983, 0.7392999889999999, 0.738300002, 0.737600005, 0.735900021, 0.735500014, 0.733899987]
t_h = [0.0, 0.08333333333333333, 0.16666666666666666, 0.25, 0.3333333333333333, 0.4166666666666667, 0.5, 0.5833333333333334, 0.6666666666666666, 0.75, 0.8333333333333334, 0.9166666666666666, 1.0, 1.0833333333333333, 1.1666666666666667, 1.25, 1.3333333333333333, 1.4166666666666667, 1.5, 1.5833333333333333, 1.6666666666666667, 1.75, 1.8333333333333333, 1.9166666666666667, 2.0, 2.0833333333333335, 2.1666666666666665, 2.25, 2.3333333333333335, 2.4166666666666665, 2.5, 2.5833333333333335, 2.6666666666666665, 2.75, 2.8333333333333335, 2.9166666666666665, 3.0, 3.0833333333333335, 3.1666666666666665, 3.25, 3.3333333333333335, 3.4166666666666665, 3.5, 3.5833333333333335, 3.6666666666666665, 3.75, 3.8333333333333335, 3.9166666666666665, 4.0, 4.083333333333333, 4.166666666666667, 4.25, 4.333333333333333, 4.416666666666667, 4.5, 4.583333333333333, 4.666666666666667, 4.75, 4.833333333333333, 4.916666666666667, 5.0, 5.083333333333333, 5.166666666666667, 5.25, 5.333333333333333, 5.416666666666667, 5.5, 5.583333333333333, 5.666666666666667, 5.75, 5.833333333333333, 5.916666666666667, 6.0, 6.083333333333333, 6.166666666666667, 6.25, 6.333333333333333, 6.416666666666667, 6.5, 6.583333333333333, 6.666666666666667, 6.75, 6.833333333333333, 6.916666666666667, 7.0, 7.083333333333333, 7.166666666666667, 7.25, 7.333333333333333, 7.416666666666667, 7.5, 7.583333333333333, 7.666666666666667, 7.75, 7.833333333333333, 7.916666666666667, 8.0, 8.083333333333334, 8.166666666666666, 8.25, 8.333333333333334, 8.416666666666666, 8.5, 8.583333333333334, 8.666666666666666, 8.75, 8.833333333333334, 8.916666666666666, 9.0, 9.083333333333334, 9.166666666666666, 9.25, 9.333333333333334, 9.416666666666666, 9.5, 9.583333333333334, 9.666666666666666, 9.75, 9.833333333333334, 9.916666666666666, 10.0, 10.083333333333334, 10.166666666666666, 10.25, 10.333333333333334, 10.416666666666666, 10.5, 10.583333333333334, 10.666666666666666, 10.75, 10.833333333333334, 10.916666666666666, 11.0, 11.083333333333334, 11.166666666666666, 11.25, 11.333333333333334, 11.416666666666666, 11.5, 11.583333333333334, 11.666666666666666, 11.75, 11.833333333333334, 11.916666666666666, 12.0, 12.083333333333334, 12.166666666666666, 12.25, 12.333333333333334, 12.416666666666666, 12.5, 12.583333333333334, 12.666666666666666, 12.75, 12.833333333333334, 12.916666666666666, 13.0, 13.083333333333334, 13.166666666666666, 13.25, 13.333333333333334, 13.416666666666666, 13.5, 13.583333333333334, 13.666666666666666, 13.75, 13.833333333333334, 13.916666666666666, 14.0, 14.083333333333334, 14.166666666666666, 14.25, 14.333333333333334, 14.416666666666666, 14.5, 14.583333333333334, 14.666666666666666, 14.75, 14.833333333333334, 14.916666666666666, 15.0, 15.083333333333334, 15.166666666666666, 15.25, 15.333333333333334, 15.416666666666666, 15.5, 15.583333333333334, 15.666666666666666, 15.75, 15.833333333333334, 15.916666666666666, 16.0, 16.083333333333332, 16.166666666666668, 16.25, 16.333333333333332, 16.416666666666668, 16.5, 16.583333333333332, 16.666666666666668, 16.75, 16.833333333333332, 16.916666666666668, 17.0, 17.083333333333332, 17.166666666666668, 17.25, 17.333333333333332, 17.416666666666668, 17.5, 17.583333333333332, 17.666666666666668, 17.75, 17.833333333333332, 17.916666666666668, 18.0, 18.083333333333332, 18.166666666666668, 18.25, 18.333333333333332, 18.416666666666668, 18.5, 18.583333333333332, 18.666666666666668, 18.75, 18.833333333333332, 18.916666666666668, 19.0, 19.083333333333332, 19.166666666666668, 19.25, 19.333333333333332, 19.416666666666668, 19.5, 19.583333333333332, 19.666666666666668, 19.75, 19.833333333333332, 19.916666666666668, 20.0, 20.083333333333332, 20.166666666666668, 20.25, 20.333333333333332, 20.416666666666668, 20.5, 20.583333333333332, 20.666666666666668, 20.75, 20.833333333333332, 20.916666666666668, 21.0, 21.083333333333332, 21.166666666666668, 21.25, 21.333333333333332]プロットします。
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
from numpy.linalg import inv
sns.set()
fig = plt.figure()
plt.rcParams['font.family'] ='sans-serif'
plt.rcParams['xtick.direction'] = 'in'
plt.rcParams['ytick.direction'] = 'in'
plt.rcParams['xtick.major.width'] = 1.0
plt.rcParams['ytick.major.width'] = 1.0
plt.rcParams['font.size'] = 9
plt.rcParams['axes.linewidth'] = 1.0
plt.gca().yaxis.set_major_formatter(plt.FormatStrFormatter('%.2f'))
plt.xlabel("time(h)")
plt.ylabel("OD600(-)")
plt.xlim(0,20)
plt.ylim(0,1.0)
unit = r"$h^{-1}$"
plt.scatter(t_h,OD600, s = 6)
plt.savefig("test.png",dpi = 500)実行結果
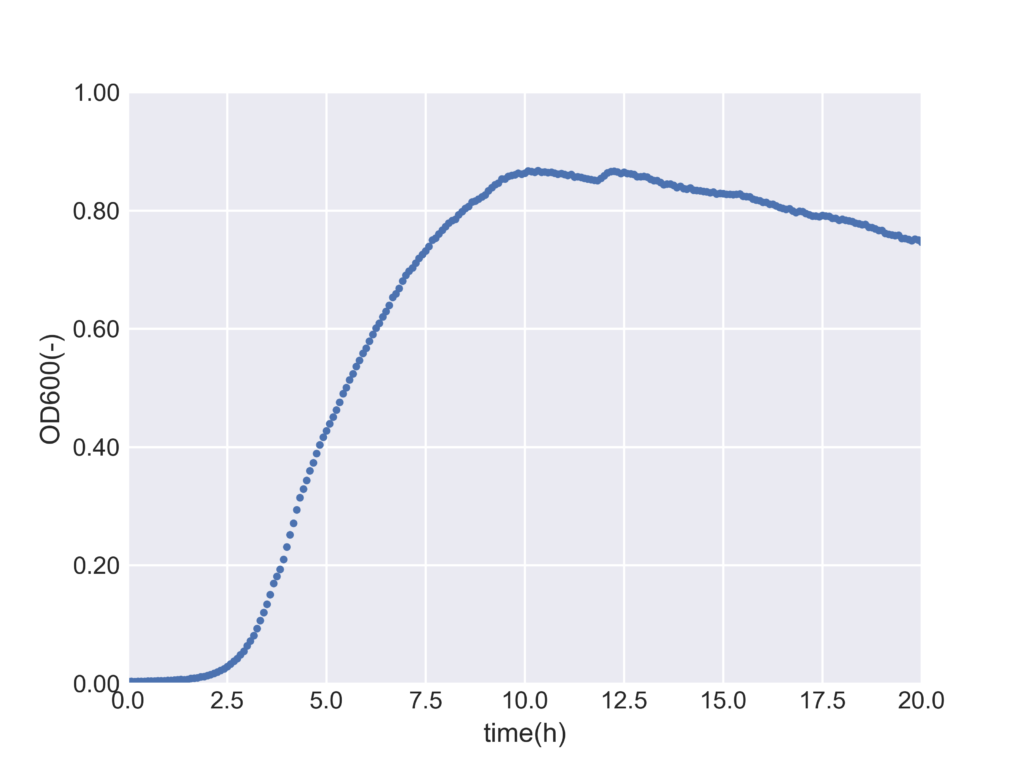
今回は対数増殖期をOD600の値が0.01から0.1の範囲とします。
filtered = [[i,j] for i,j in zip(t_h,OD600) if 0.01 <= j <= 0.1]
t_h, OD600 = [i[0] for i in filtered],[i[1] for i in filtered]
plt.scatter(t_h,OD600, s = 6)
plt.xlim(min(t_h) -0.1,max(t_h)+0.1)
plt.ylim(min(OD600) -0.05,max(OD600)+0.05)
plt.savefig("test.png",dpi = 500)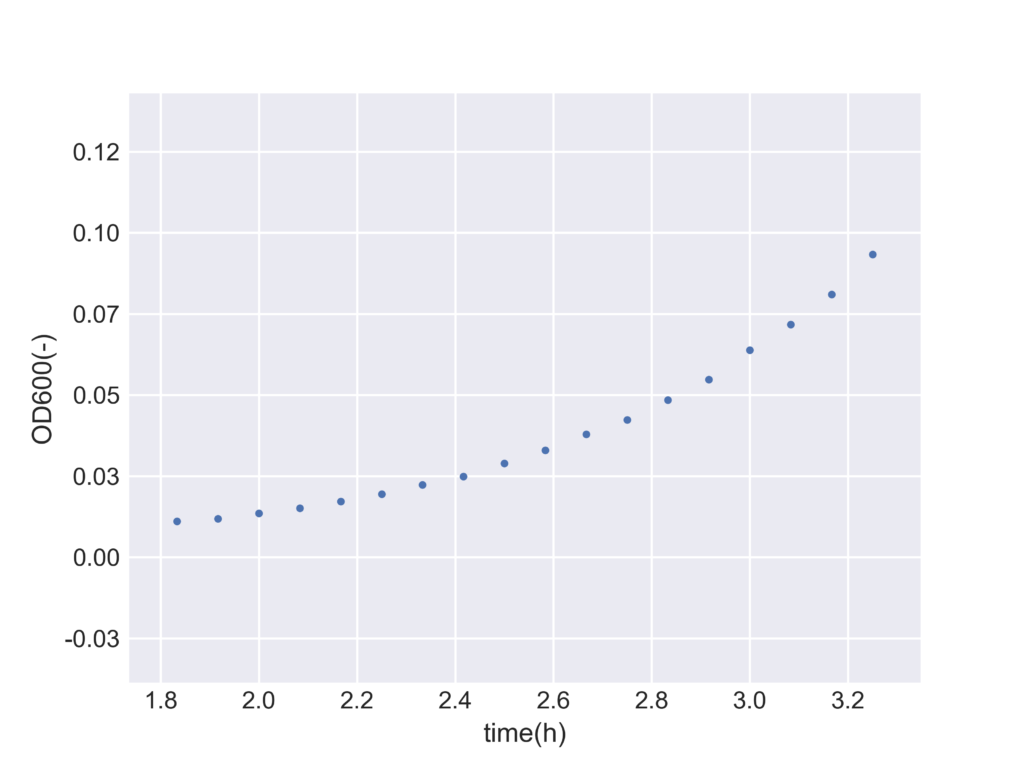
正規方程式を使用してパラメータを決定します。
filtered = [[i,j] for i,j in zip(t_h,OD600) if 0.01 <= j <= 0.1]
t_h, OD600 = [i[0] for i in filtered],[i[1] for i in filtered]
f = np.array([np.log(i) for i in OD600]).T
W = np.array([[i,1] for i in t_h])
W_t = W.T
theta = inv(W_t@W)@W_t@f
X = t_h
Y = [np.exp(theta[0]*i + theta[1]) for i in t_h]
plt.plot(X,Y,color='red')
plt.scatter(t_h,OD600, s = 6)
plt.xlim(min(t_h) -0.1,max(t_h)+0.1)
plt.ylim(min(OD600) -0.05,max(OD600)+0.05)
plt.savefig("test.png",dpi = 500)実行結果
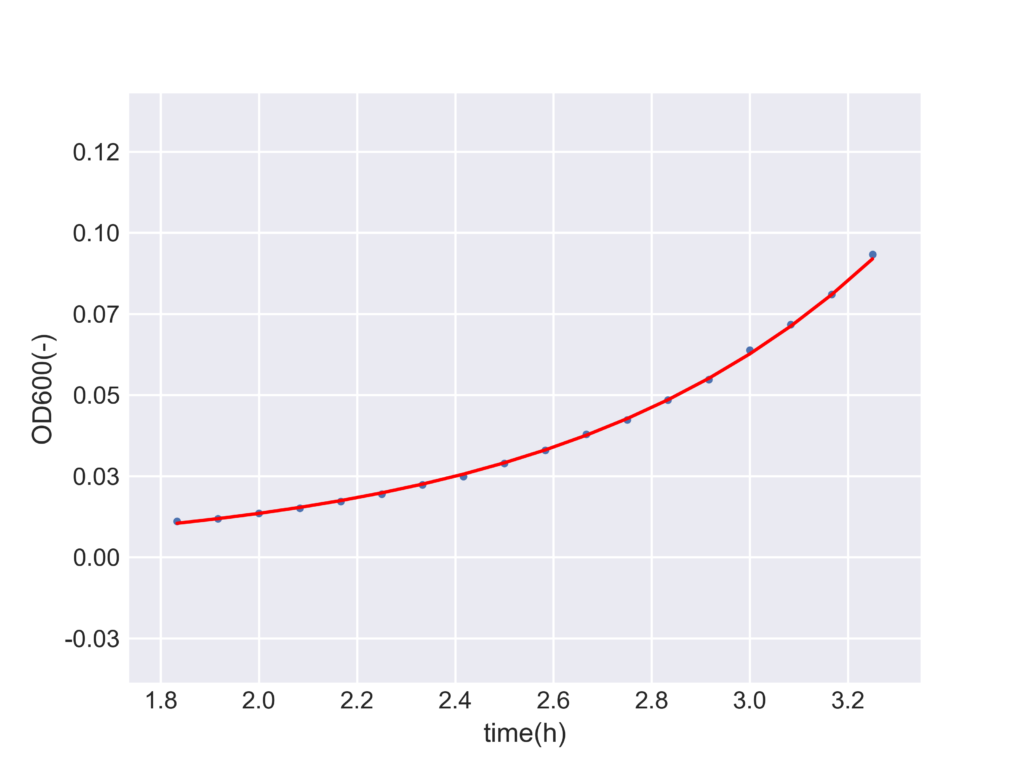
よってこの細胞の比増殖速度は1.53(1/h)であることがわかりました。



