一般に、4次元以上のデータを可視化することは不可能なので、高次元データを可視化する方法の一つとしてPCAという手法が使われています。
今回はわかりやすいように、2次元のデータを1次元に圧縮します。
目次
二次元ガウス分布の生成
初めに、以下のように二次元ガウス分布を作成します。
import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import multivariate_normal
seed_value = 42
np.random.seed(seed_value)
# 二次元正規分布の平均と共分散行列を定義
mean = [0, 0]
covariance = [[1, 0.5], [0.5, 1]]
# 二次元正規分布を生成
rv = multivariate_normal(mean, covariance)
# プロットする範囲を指定
x = np.linspace(-3, 3, 400)
y = np.linspace(-3, 3, 400)
X, Y = np.meshgrid(x, y)
pos = np.dstack((X, Y))
# 二次元正規分布の確率密度関数を計算
Z = rv.pdf(pos)
# プロット
fig = plt.figure()
plt.contourf(X, Y, Z, levels=20, cmap='inferno')
plt.colorbar(label='Probability Density')
plt.xlabel('X')
plt.ylabel('Y')
fig.savefig("result1.png",dpi= 500)実行結果
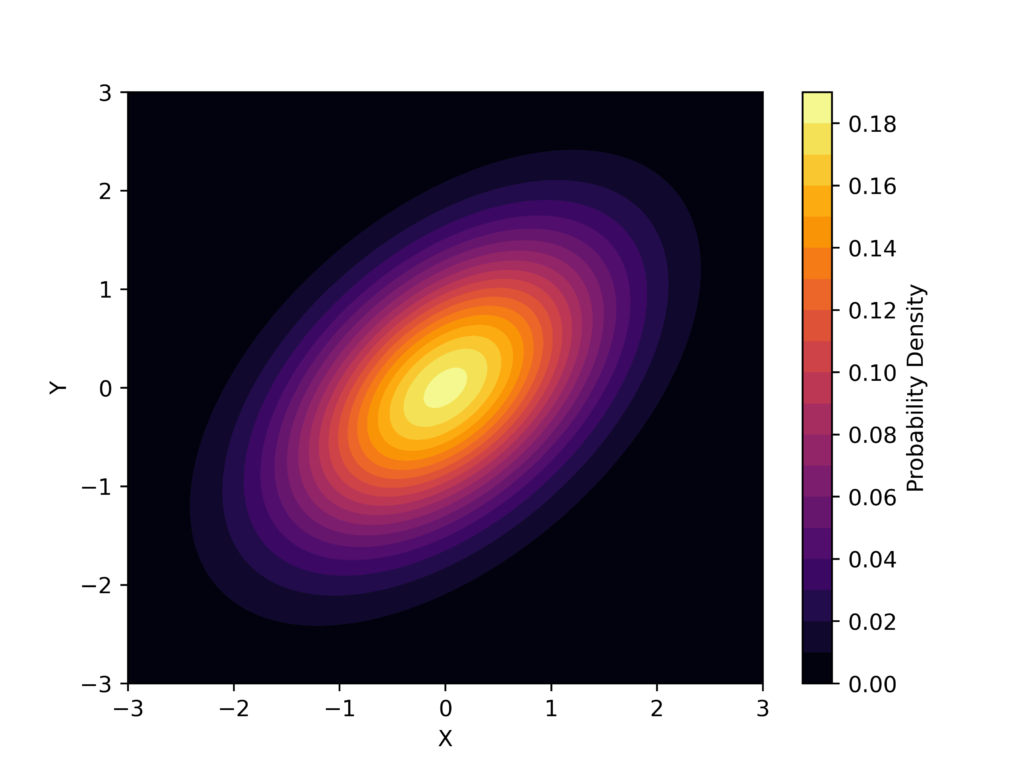
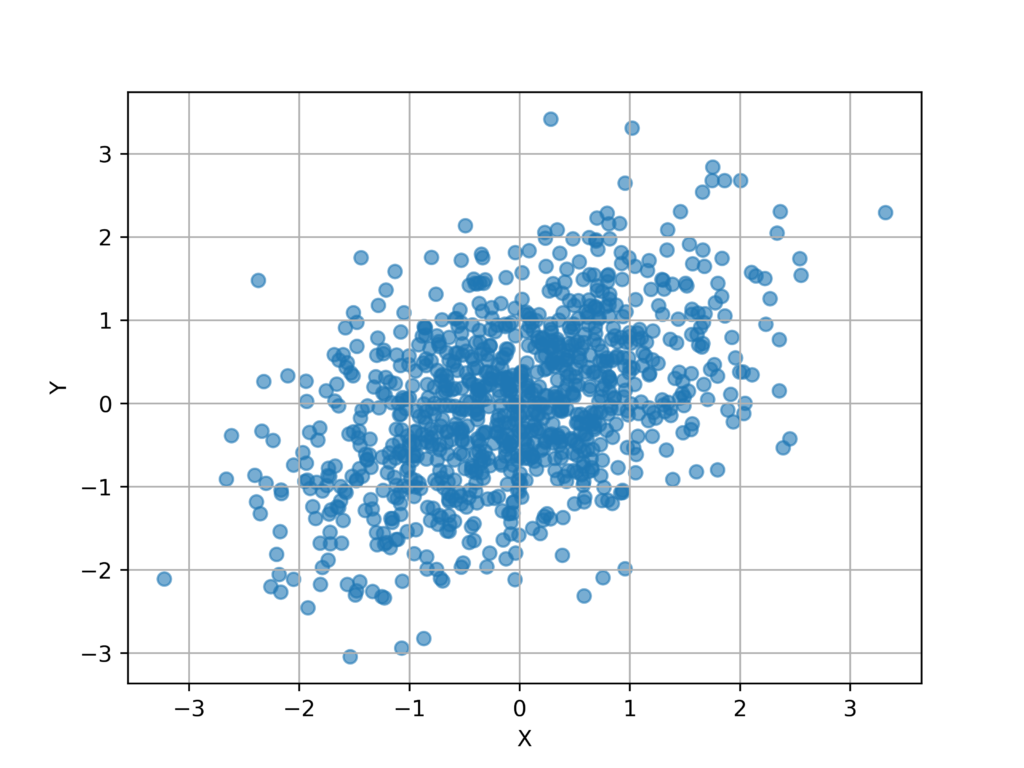
上記のガウス分布からシード値を固定して1000個の点をランダムにサンプリングします。
import matplotlib.pyplot as plt
from scipy.stats import multivariate_normal
import numpy as np
seed_value = 42
np.random.seed(seed_value)
# 二次元正規分布の平均と共分散行列を定義
mean = [0, 0]
covariance = [[1, 0.5], [0.5, 1]]
# 二次元正規分布を生成
rv = multivariate_normal(mean, covariance)
# プロットする点の数
num_points = 1000
# 乱数を生成して二次元正規分布からサンプリング
samples = rv.rvs(size=num_points)
# サンプルした点のx座標とy座標を取得
x_samples = samples[:, 0]
y_samples = samples[:, 1]
# プロット
fig = plt.figure()
plt.scatter(x_samples, y_samples, alpha=0.6)
plt.xlabel('X')
plt.ylabel('Y')
plt.grid(True)
fig.savefig("result.png",dpi = 500)実行結果
分散共分散行列の作成
分散共分散行列は以下のように定義されます。
$\Sigma = V[\mathbf{X}] = \begin{pmatrix} V[\mathbf{X}_1]& Cov[\mathbf{X_1},\mathbf{X_2}] \\ Cov[\mathbf{X_1},\mathbf{X_2}]& V[\mathbf{X}_2] \end{pmatrix}$
これをpythonで作成すると以下のようになります。
X = np.array([x_samples,y_samples])
Cov = np.cov(X)
>>>
[[0.95323054 0.43597516]
[0.43597516 0.94886213]]次元の圧縮
今回は次元を2次元から1次元に圧縮するので、以下のような線型写像
$\mathbb{R}^2 \mapsto \mathbb{R}$
について考えます。
ここで、線形変換を行う射影行列を
$\mathbf{w} = (w_1…\:w_n)^\mathrm{T}$
とすると、次元圧縮後のベクトルの分散は
$s ^2 = \mathbf{w}^\mathrm{T} \Sigma \mathbf{w}$
と表すことができます。
次元を圧縮する際に寄与率が最大となるためには、この分散を最大化すれば良いので、
$\arg \max(\mathbf{w}^\mathrm{T} \Sigma \mathbf{w}) ,\: \mathbf{w}^\mathrm{T} \mathbf{w} = 1$
について考えれば良いことになります。
ここで、射影後の分散が発散してしまわないように、射影行列のノルムを1に固定しています。
上記の制約付き最大化問題について、ラグランジュの未定数法を用いると、
$\mathcal{L}(\mathbf{w},\lambda) = \mathbf{w}^\mathrm{T} \Sigma \mathbf{w} – \lambda (\mathbf{w}^\mathrm{T}\mathbf{w}-1)$
上式から
$\frac{\partial \mathcal{L}}{\partial \mathbf{w}} = 2\Sigma\mathbf{w}-2\lambda\mathbf{w} = 0$
の時が射影後の分散を最大化できることがわかります。
よって、
$\Sigma \mathbf{w} = \lambda \mathbf{w}$
これを変形すると
$s^2 = \lambda$
となります。
上記から、固有方程式
$ \det(\Sigma -\lambda \mathbf{I}) = 0$
を解くことによって、以下の固有空間を張る基底を求めることができます。
$\mathbf{W}_{\lambda_i} = {c\mathbf{v}_i | c\in \mathbb{R}, \: \lambda_i \notin \mathbb{C} }$
これらの基底のうち、固有値が最大となるものを第一主成分軸とします。
このとき、第一主成分軸の元のデータへの寄与率は以下の式で求めることができます。
$PC_1 = \frac{\lambda_ {max} }{Tr(\Lambda)}$
また、射影後のベクトルは以下のようにして求めることができます。
$\mathbf{U}_{PC1} = \mathbf{X}\mathbf{w} \in \mathbb{R}$
これは二次元から一次元の場合にのみ使えますが、n次元に一般化すると固有値の大きい順から削減したい次元数だけwの列ベクトルを並べた行列によって計算することができます。
$\mathbf{U}_{PC1} = \mathbf{X}\mathbf{Q} \in \mathbb{R^n}$
Pythonで実装
上記の処理をpythonで実装します。
import matplotlib.pyplot as plt
from scipy.stats import multivariate_normal
import numpy as np
from numpy.linalg import eig
import math
import pandas as pd
import seaborn as sns
seed_value = 42
np.random.seed(seed_value)
# 二次元正規分布の平均と共分散行列を定義
mean = [0, 0]
covariance = [[1, 0.5], [0.5, 1]]
# 二次元正規分布を生成
rv = multivariate_normal(mean, covariance)
# プロットする点の数
num_points = 1000
# 乱数を生成して二次元正規分布からサンプリング
samples = rv.rvs(size=num_points)
# サンプルした点のx座標とy座標を取得
x_samples = samples[:, 0]
y_samples = samples[:, 1]
X = np.array([x_samples,y_samples])
Sigma = np.cov(X)
eigenvalues, eigenvectors = eig(Sigma)
if eigenvalues[1] < eigenvalues[0]:
m = eigenvectors[0][0]/eigenvectors[1][0]
k_t = 0
PC1 = eigenvalues[0]/(sum(eigenvalues))
Q = np.array(eigenvectors[1])
w = eigenvectors[0]
else:
m = eigenvectors[0][1]/eigenvectors[1][1]
k_t = 0
PC1 = eigenvalues[1]/(sum(eigenvalues))
Q = np.array(eigenvectors[0])
w = eigenvectors[1]
print(eigenvalues)
print(eigenvectors)
#元のプロットに第一主成分を重ね合わせる
fig = plt.figure()
x = np.linspace(-5,5,1000)
plt.scatter(x_samples, y_samples, alpha=0.6)
plt.scatter(x,[i*m+k_t for i in x],s = 2,color = "red")
plt.xlabel(f'X')
plt.ylabel('Y')
plt.title(f"PC1: {math.floor((PC1*1000))/10}%")
plt.grid(True)
fig.savefig("result3.png",dpi = 500)
plt.close()
#射影
U = X.transpose()@np.array(eigenvectors[0])
df = pd.DataFrame({
'U_PC1': U,
})
df_melt = pd.melt(df)
print(df_melt.head())
#JItterプロット
fig = plt.figure()
ax = fig.add_subplot(1, 1, 1)
sns.stripplot(x='variable', y='value', data=df_melt, jitter=True, color='black', ax=ax)
ax.set_ylabel('U')
ax.set_xlabel('Prob. density(-)')
ax.set_ylim(min(U)-1,max(U)+1)
ax.set_title(f"PC1: {math.floor((PC1*1000))/10}%")
ax.grid()
fig.savefig("jitter_plot.png",dpi = 500)
#バイオリンプロット
fig = plt.figure()
ax = fig.add_subplot(1, 1, 1)
sns.violinplot(x='variable', y='value', data=df_melt, jitter=True, ax=ax)
ax.set_ylabel('U')
ax.set_xlabel('Prob. density(-)')
ax.set_ylim(min(U)-1,max(U)+1)
ax.set_title(f"PC1: {math.floor((PC1*1000))/10}%")
ax.grid()
fig.savefig("Violin.png",dpi = 500)
#ボックスプロット
fig = plt.figure()
ax = fig.add_subplot(1, 1, 1)
sns.boxplot(x='variable', y='value', data=df_melt, showfliers=False, ax=ax, color='white', width=0.2)
ax.set_ylabel('U')
ax.set_xlabel('Prob. density(-)')
ax.set_ylim(min(U)-1,max(U)+1)
ax.set_title(f"PC1: {math.floor((PC1*1000))/10}%")
fig.savefig("box_plot.png",dpi = 500)
実行結果
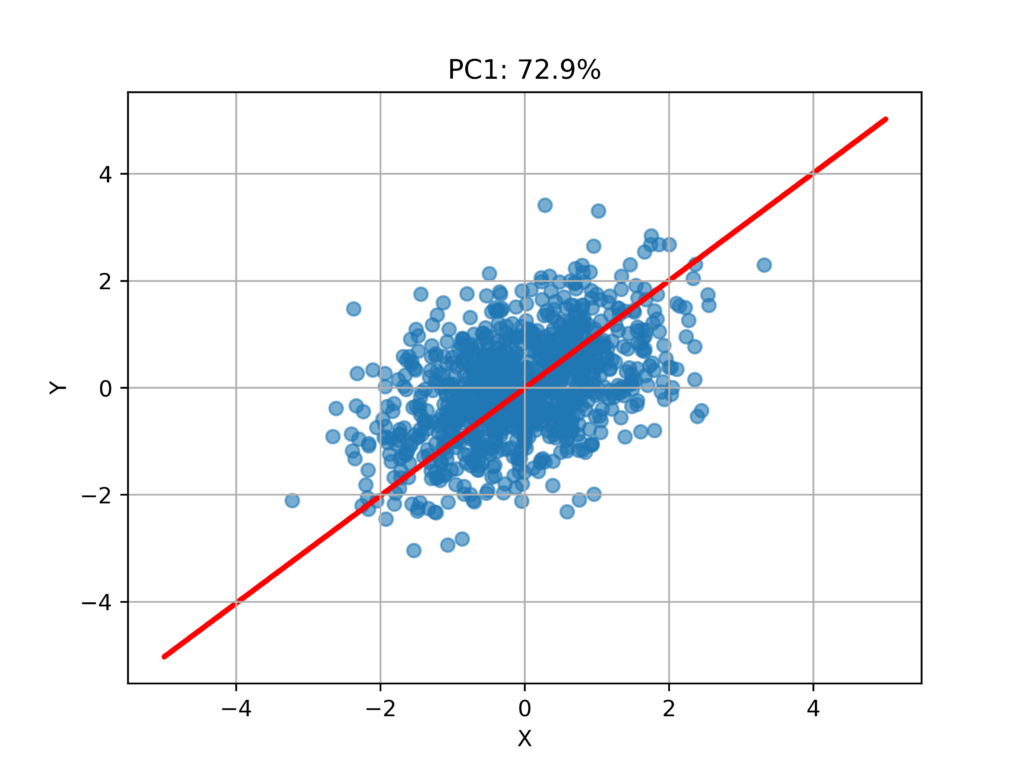
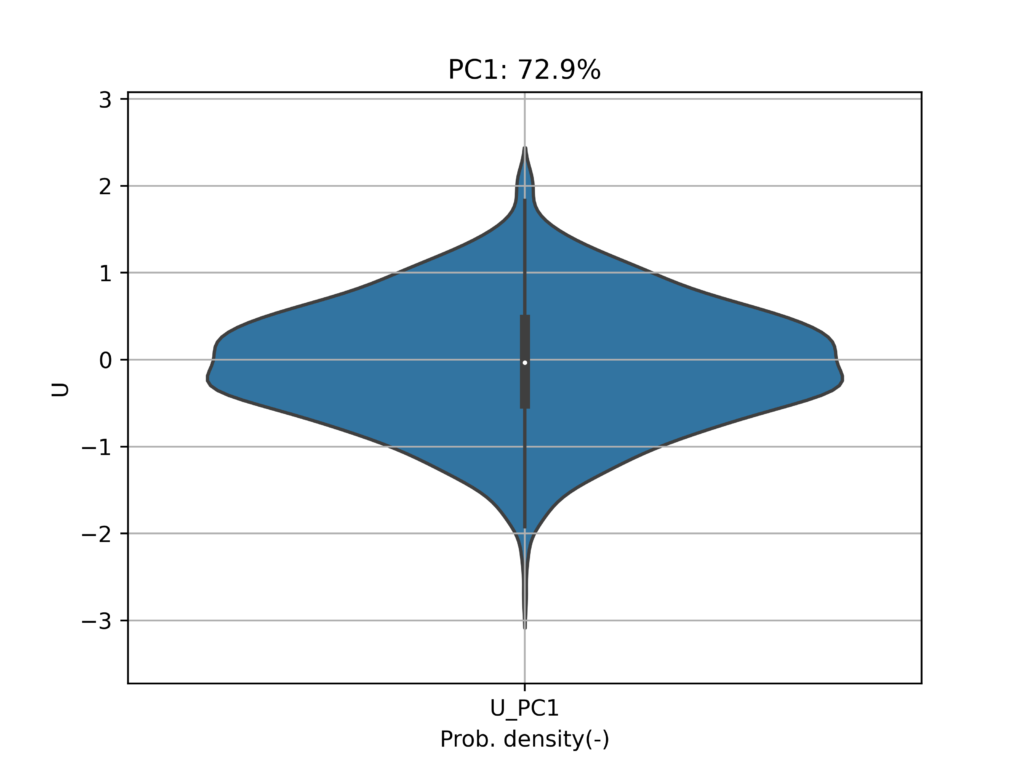
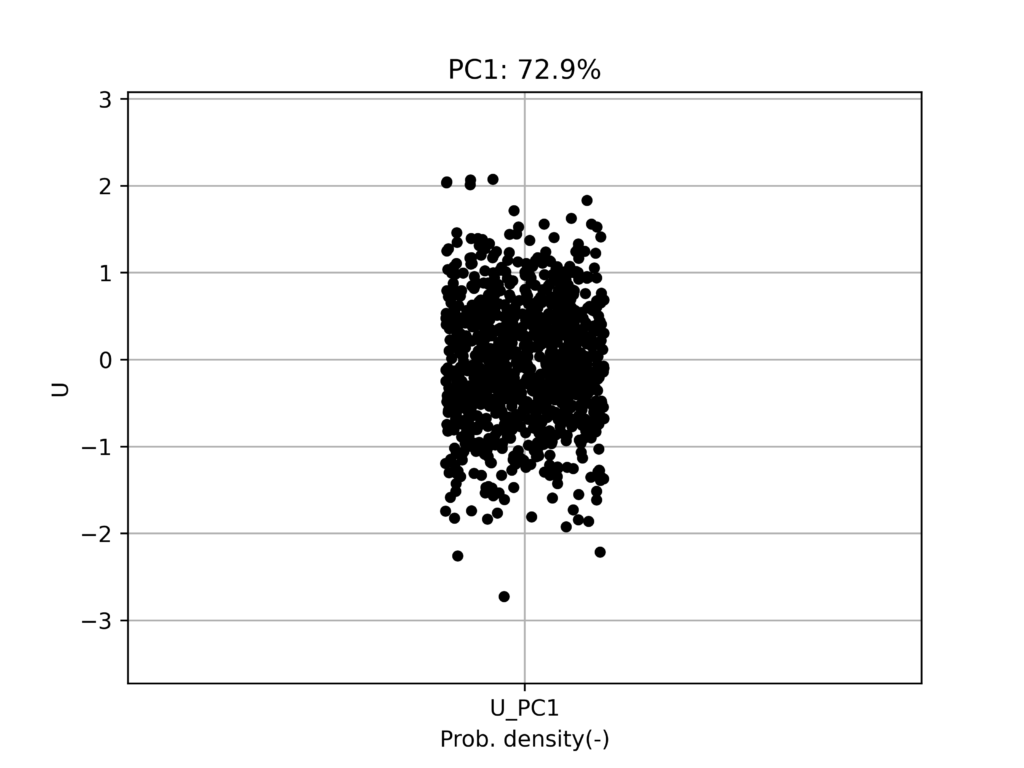
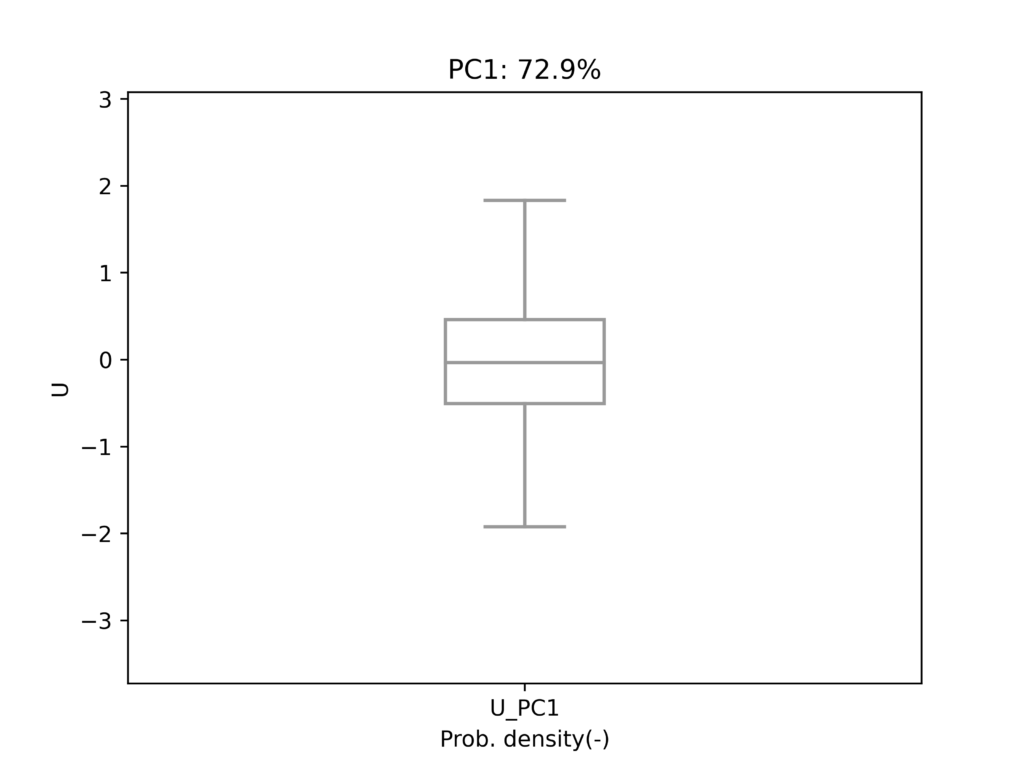
射影結果
一次元情報は分かりにくいので、バイオリンプロット等を使用して可視化してみます。