画像解析の際、細胞に限らず、物体の方向を捉えたいという場面はたくさんあります。このような時に、その方向を高速計算するアルゴリズムについて考えます。
今回は細胞を使用して、その伸長方向を決定します。
目次
細胞の情報
以下のような輪郭座標の点群で与えられるデータを細胞とします。
[[136, 121], [135, 122], [134, 122], [133, 123], [132, 123], [132, 124], [131, 125], [131, 126], [130, 127], [130, 128], [129, 129], [130, 130], [130, 131], [130, 132], [130, 133], [131, 134], [131, 135], [132, 136], [132, 137], [132, 138], [133, 139], [133, 140], [134, 141], [134, 142], [135, 143], [135, 144], [136, 145], [136, 146], [137, 147], [137, 148], [138, 149], [138, 150], [139, 151], [140, 152], [140, 153], [141, 154], [142, 155], [142, 156], [143, 157], [144, 158], [145, 159], [145, 160], [146, 161], [146, 162], [147, 163], [147, 164], [148, 165], [148, 166], [149, 167], [150, 168], [150, 169], [151, 170], [151, 171], [152, 172], [153, 173], [153, 174], [154, 175], [154, 176], [155, 177], [155, 178], [156, 179], [157, 180], [158, 180], [159, 180], [160, 180], [161, 180], [162, 180], [163, 180], [164, 180], [165, 180], [166, 179], [167, 179], [168, 178], [168, 177], [168, 176], [169, 175], [169, 174], [169, 173], [169, 172], [169, 171], [169, 170], [169, 169], [169, 168], [169, 167], [169, 166], [169, 165], [168, 164], [168, 163], [168, 162], [167, 161], [167, 160], [166, 159], [166, 158], [165, 157], [164, 156], [164, 155], [163, 154], [162, 153], [162, 152], [161, 151], [161, 150], [160, 149], [159, 148], [159, 147], [158, 146], [157, 145], [157, 144], [156, 143], [156, 142], [155, 141], [154, 140], [154, 139], [153, 138], [152, 137], [152, 136], [151, 135], [150, 134], [150, 133], [149, 132], [149, 131], [149, 130], [148, 129], [147, 128], [147, 127], [146, 126], [145, 125], [145, 124], [144, 124], [143, 123], [142, 123], [141, 122], [140, 122], [139, 121], [138, 121], [137, 121]]この細胞の情報をpythonで可視化してみます。
import matplotlib.pyplot as plt
import numpy as np
cell = [[136, 121], [135, 122], [134, 122], [133, 123], [132, 123], [132, 124], [131, 125], [131, 126], [130, 127], [130, 128], [129, 129], [130, 130], [130, 131], [130, 132], [130, 133], [131, 134], [131, 135], [132, 136], [132, 137], [132, 138], [133, 139], [133, 140], [134, 141], [134, 142], [135, 143], [135, 144], [136, 145], [136, 146], [137, 147], [137, 148], [138, 149], [138, 150], [139, 151], [140, 152], [140, 153], [141, 154], [142, 155], [142, 156], [143, 157], [144, 158], [145, 159], [145, 160], [146, 161], [146, 162], [147, 163], [147, 164], [148, 165], [148, 166], [149, 167], [150, 168], [150, 169], [151, 170], [151, 171], [152, 172], [153, 173], [153, 174], [154, 175], [154, 176], [155, 177], [155, 178], [156, 179], [157, 180], [158, 180], [159, 180], [160, 180], [161, 180], [162, 180], [163, 180], [164, 180], [165, 180], [166, 179], [167, 179], [168, 178], [168, 177], [168, 176], [169, 175], [169, 174], [169, 173], [169, 172], [169, 171], [169, 170], [169, 169], [169, 168], [169, 167], [169, 166], [169, 165], [168, 164], [168, 163], [168, 162], [167, 161], [167, 160], [166, 159], [166, 158], [165, 157], [164, 156], [164, 155], [163, 154], [162, 153], [162, 152], [161, 151], [161, 150], [160, 149], [159, 148], [159, 147], [158, 146], [157, 145], [157, 144], [156, 143], [156, 142], [155, 141], [154, 140], [154, 139], [153, 138], [152, 137], [152, 136], [151, 135], [150, 134], [150, 133], [149, 132], [149, 131], [149, 130], [148, 129], [147, 128], [147, 127], [146, 126], [145, 125], [145, 124], [144, 124], [143, 123], [142, 123], [141, 122], [140, 122], [139, 121], [138, 121], [137, 121]]
x = [i[0] for i in cell]
y = [i[1] for i in cell]
center = [np.mean(y),np.mean(x)]
X = np.array([y,x])
fig = plt.figure(figsize=(10,10))
plt.xlim(100,200)
plt.ylim(100,200)
plt.scatter(x,y,s = 40,color = "lime")
plt.scatter(center[1],center[0],s = 40,color = "red")
plt.grid()
fig.savefig("test.png",dpi=300)実行結果
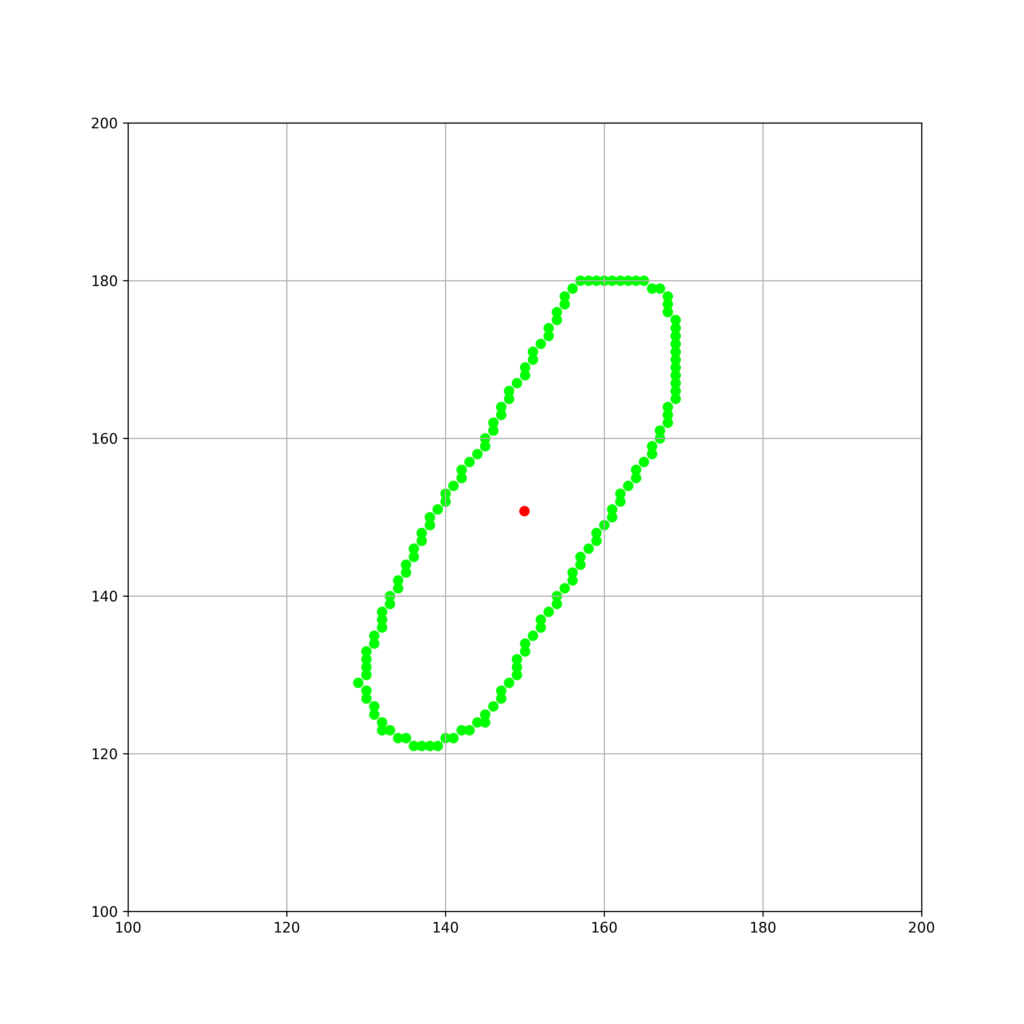
今回はこの細胞に関して、進行方向、つまり中心軸となるような直線を数学的に決定してみます。
アルゴリズム
細胞が伸長する方向は一定であると仮定します。
この時、その伸長方向を、ある射影ベクトルを用いて線形変換を行った結果、その分散が最大となるものと定義します。
細胞の座標及び、射影ベクトルを以下のように定義すると、
$$\mathbf{X} = \begin{pmatrix}x_1 & \cdots&x_n \\y_1 &\cdots & y_n\end{pmatrix}^\mathrm{T}\in \mathbb{R}^{n\times 2} $$
$$\mathbf{w} = \begin{pmatrix}w_1 & w_2\end{pmatrix}^\mathrm{T}\in \mathbb{R}^2$$
射影ベクトルで線形変換後のデータの分散を、以下のように分散共分散行列によって表すことができます。
$$\Sigma = \begin{pmatrix}V[\mathbf{X_1}] &Cov[\mathbf{X_1},\mathbf{X_2}] \\Cov[\mathbf{X_1},\mathbf{X_2}]s & V[\mathbf{X_2}]\end{pmatrix}$$
$$s^2 = \mathbf{w}^\mathrm{T}\Sigma \mathbf{w}$$
この分散の値を最大化する射影後のベクトルは細胞の長軸、つまり伸長方向に対応すると考えることができるため、上式の最大化問題について考えます。
この時、分散が発散する可能性があるため、射影行列のノルムを固定しておきます。
よって、以下の制約付き最大化問題を解くことになります。
$$\arg \max (\mathbf{w}^\mathrm{T}\Sigma \mathbf{w}),\: \|\mathbf{w}\| = 1$$
上記から、ラグランジュの未定乗数法により、
$$\mathcal{L}(\mathbf{w},\lambda) = \mathbf{w}^\mathrm{T}\Sigma \mathbf{w} – \lambda(\mathbf{w}^\mathrm{T}\mathbf{w}-1)$$
分散が最大化する時、
$$\frac{\partial \mathcal{L}}{\partial\mathbf{w}} = 2\Sigma\mathbf{w}-2\lambda\mathbf{w} = 0$$
従って、固有方程式
$$\det (\Sigma -\lambda \mathbf{I}) = 0$$
を解くことによって、
$$\mathbf{W}_{\lambda_i} = \{c\mathbf{v_i}|c\in \mathbb{R},\:\lambda_i\notin \mathbb{C}\}\in \mathbb{R}^2$$
を張る2本の基底を得ることができます。
この時、固有値が大きい方に対応する固有ベクトルを細胞の伸長方向とします。
実装
上記の理論をもとに、伸長方向を計算します。
import matplotlib.pyplot as plt
import numpy as np
from numpy.linalg import eig
cell = [[136, 121], [135, 122], [134, 122], [133, 123], [132, 123], [132, 124], [131, 125], [131, 126], [130, 127], [130, 128], [129, 129], [130, 130], [130, 131], [130, 132], [130, 133], [131, 134], [131, 135], [132, 136], [132, 137], [132, 138], [133, 139], [133, 140], [134, 141], [134, 142], [135, 143], [135, 144], [136, 145], [136, 146], [137, 147], [137, 148], [138, 149], [138, 150], [139, 151], [140, 152], [140, 153], [141, 154], [142, 155], [142, 156], [143, 157], [144, 158], [145, 159], [145, 160], [146, 161], [146, 162], [147, 163], [147, 164], [148, 165], [148, 166], [149, 167], [150, 168], [150, 169], [151, 170], [151, 171], [152, 172], [153, 173], [153, 174], [154, 175], [154, 176], [155, 177], [155, 178], [156, 179], [157, 180], [158, 180], [159, 180], [160, 180], [161, 180], [162, 180], [163, 180], [164, 180], [165, 180], [166, 179], [167, 179], [168, 178], [168, 177], [168, 176], [169, 175], [169, 174], [169, 173], [169, 172], [169, 171], [169, 170], [169, 169], [169, 168], [169, 167], [169, 166], [169, 165], [168, 164], [168, 163], [168, 162], [167, 161], [167, 160], [166, 159], [166, 158], [165, 157], [164, 156], [164, 155], [163, 154], [162, 153], [162, 152], [161, 151], [161, 150], [160, 149], [159, 148], [159, 147], [158, 146], [157, 145], [157, 144], [156, 143], [156, 142], [155, 141], [154, 140], [154, 139], [153, 138], [152, 137], [152, 136], [151, 135], [150, 134], [150, 133], [149, 132], [149, 131], [149, 130], [148, 129], [147, 128], [147, 127], [146, 126], [145, 125], [145, 124], [144, 124], [143, 123], [142, 123], [141, 122], [140, 122], [139, 121], [138, 121], [137, 121]]
x = [i[0] for i in cell]
y = [i[1] for i in cell]
center = [np.mean(y),np.mean(x)]
X = np.array([y,x])
fig = plt.figure(figsize=(10,10))
plt.xlim(100,200)
plt.ylim(100,200)
plt.scatter(x,y,s = 40,color = "lime")
plt.scatter(center[1],center[0],s = 40,color = "red")
plt.grid()
Sigma = np.cov(X)
eigenvalues, eigenvectors = eig(Sigma)
m = eigenvectors[1][1]/eigenvectors[1][0] if eigenvectors[1][0] != 0 else eigenvectors[0][1]/eigenvectors[0][0]
plt.scatter([np.linspace(100,200,1000)],[m*i - m*center[1] + center[0] for i in np.linspace(100,200,1000)],s = 1,color = "blue")
fig.savefig("test.png",dpi=300)
実行結果
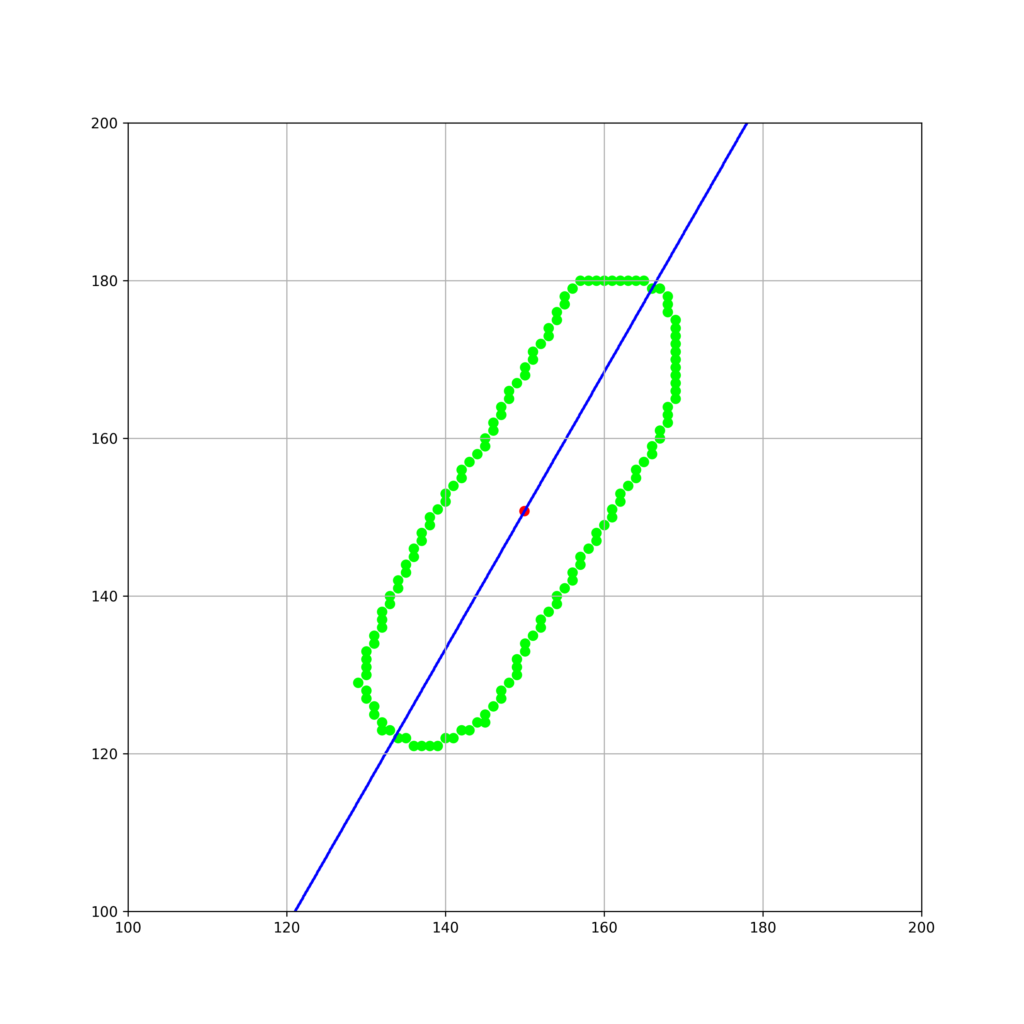
考えたアルゴリズムによって、伸長方向を計算することができました。