ANNsによる回帰【機械学習】

単純回帰

一つの変数によって目的変数を予測する単純な回帰は以下のように表されます。

$$y_i = \beta_0 + \beta_1 x_i + \epsilon_i$$

これをパーセプトロンを使って書くと、

$$\hat{y}_i = \sigma (w_0+\mathbf{x}^\mathrm{T}\mathbf{w})=\sigma (\mathbf{x}^\mathrm{T}\mathbf{w})$$

Pytorchでランダムプロットの生成

回帰用にtorchを使用してランダムプロットを生成します。

import numpy as np 
import torch 
import torch.nn as nn 
import matplotlib.pyplot as plt 

fig = plt.figure()

N = 30
x = torch.randn(N,1)
y = x + torch.randn(N,1)/2

plt.scatter(x,y)
plt.grid()
plt.xlabel("x")
plt.ylabel("y")
fig.savefig('a.png',dpi = 500)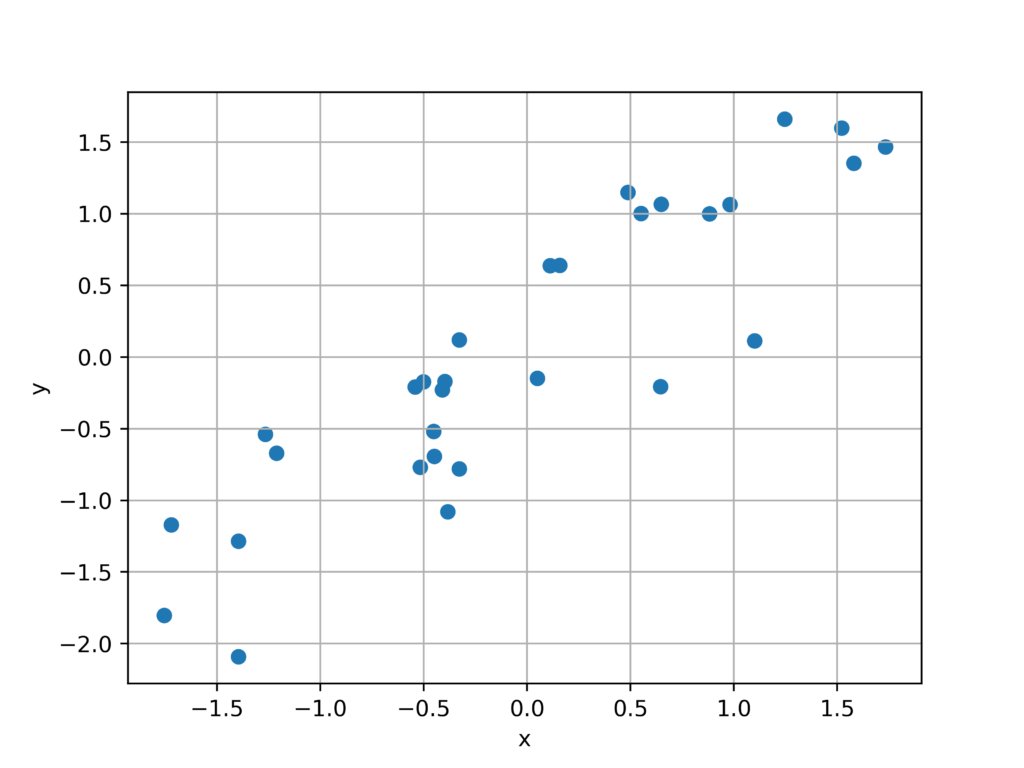

回帰モデルの設定

今回はインプット層、アウトプット層は両方一つを受け取って一つを返す返す形なので、パラメータは１にしています。

ANNModel = nn.Sequential(
    nn.Linear(1,1),  # インプット層
    nn.ReLU(),       # 活性化関数
    nn.Linear(1,1)   # アウトプット層
    )

パラメータの設定

#学習率
lr = 0.05
#損失関数(最小二乗誤差)
L = nn.MSELoss()
#最適化
optimizer = torch.optim.SGD(ANNModel.parameters(),lr=lr)

学習

epochs = 500
#損失の初期化
losses = torch.zeros(epochs)

#学習
for i in range(epochs):
    #Forward pass
    Y_hat = ANNModel(x)

    #損失の計算
    loss = L(Y_hat,y)
    losses[i] = loss

    # Back propagation
    optimizer.zero_grad()
    loss.backward()
    optimizer.step()

predictions = ANNModel(x)

finalloss = (predictions-y).pow(2).mean()

勾配の収束の様子をプロット

plt.plot(losses.detach(),'o',markerfacecolor='w',linewidth=.1)
plt.plot(epochs,finalloss.detach(),'-o')
plt.xlabel('Epoch')
plt.ylabel('Loss')
plt.title('Final loss = %g' %finalloss.item())
plt.grid()
fig.savefig("a.png",dpi = 500)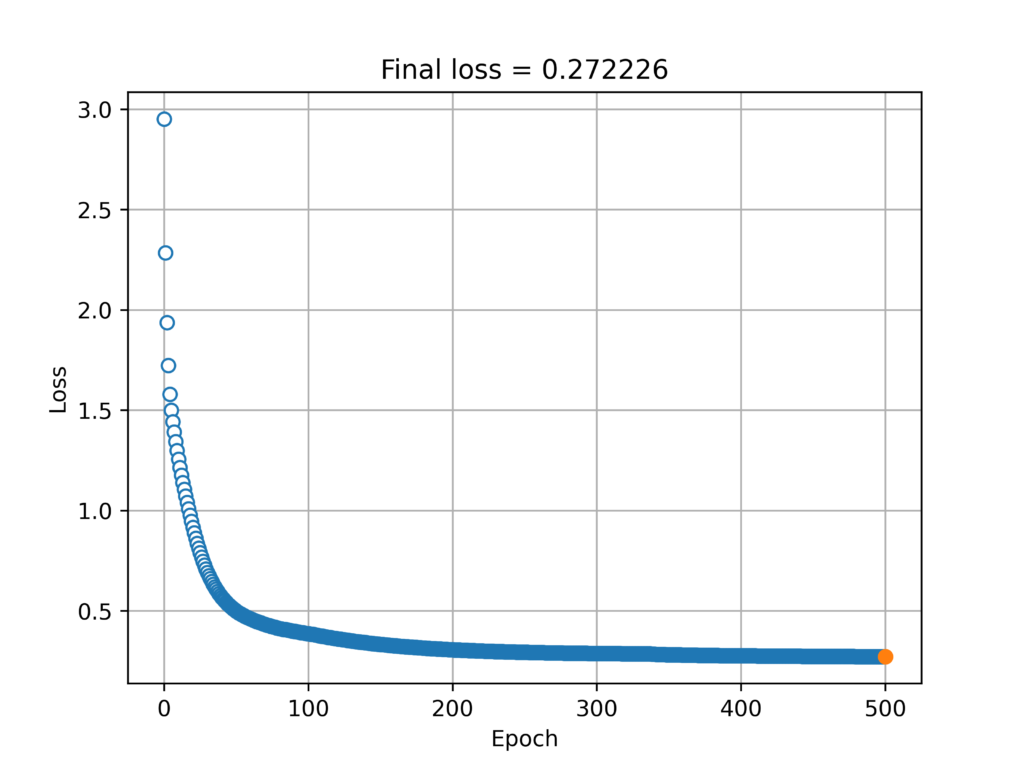

学習結果を出力してみます。

plt.plot(x,y,'bo',label='Real data',color = "black")
plt.plot(x,predictions.detach(),'rs',label='Predictions',color ="red")
plt.title(f'r={np.corrcoef(y.T,predictions.detach().T)[0,1]:.2f}')
plt.legend()
fig.savefig("a.png",dpi = 500)