目次
ネットワークの描画
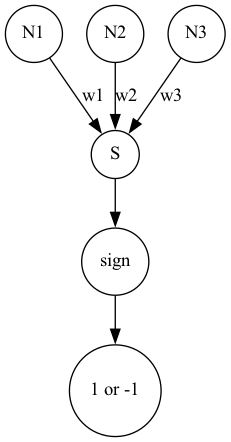
Pythonを使用して、3つの入力に対して重みをかけて計算した結果を出力するネットワークを以下のように描画します。
from graphviz import Digraph
G2 = Digraph(format="png")
G2.attr("node", shape="circle")
G2.edge(r"N1",r"S","w1")
G2.edge(r"N2",r"S","w2")
G2.edge(r"N3",r"S","w3")
G2.edge(r"S",r"sign")
G2.edge(r"sign","1 or -1")
G2.render("data")
>>>
Forward Propagation
図において、
$$\mathbf{X} = (N_1,N_2,N_3)^\mathrm{T}$$
$$\mathbf{W} = (w_1,w_2,w_3)^\mathrm{T}$$
とすると、ANNsは
$$\hat{\mathbf{y}} = \sigma(\mathbf{X}^\mathrm{T}\mathbf{W} )$$
と表せます。
バイアスを加味した場合、ネットワークは以下のようになります。
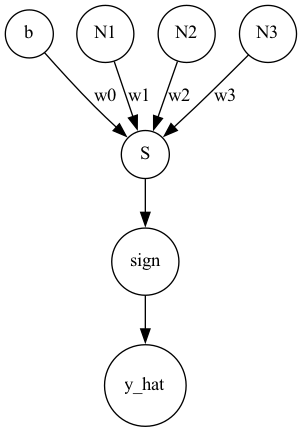
これを数式で表すと、
$$\hat{\mathbf{y}} = \sigma(\mathbf{X}^\mathrm{T}\mathbf{W} +\mathbf{b}\mathbf{w_0})$$
となります。
通常はバイアス部分は一つにまとめて、
$$\hat{\mathbf{y}} = \sigma(\mathbf{X}^\mathrm{T}\mathbf{W} +\mathbf{w_0})$$
と表すことが多いようです。
損失評価
実測値と予測値の差を評価する方法はたくさんありますが、以下の2つがよく使われています。
最小二乗誤差
$$\mathcal{L}=\frac{1}{2}(\hat{y}-y)^2$$
身長、家の価格、温度などに使用
交差エントロピー誤差
$$\mathcal{L}= -(y\log {\hat{y}} + (1-y)\log (1-\hat{y}))$$
コスト関数
$$\mathcal{J} = \frac{1}{n}\sum_{i=1}^n \mathcal{L}(\hat{y}_i,y_i)$$
Back Propagation
入力に対して、
$$\sigma (\mathbf{x}^\mathbf{T}\mathbf{w}) \to \hat{y}$$
が計算される時、予測値を変更可能なパラメータは$\mathbf{w}$のみですが、この値を以下のように更新します。(勾配降下法)
$$\mathbf{w} \leftarrow \mathbf{w} – \eta \partial \mathcal{L}$$
ここで、$\eta$は学習率であり、偏微分項は
$$\frac{\partial \mathcal{L}\sigma(\hat{y},y)}{\partial \mathbf{w}} = \frac{\partial \mathcal{L} ( \sigma(\mathbf{x}^\mathrm{T}\mathbf{w} ),y)}{\partial \mathbf{w}}$$
最小二乗誤差の場合
最小二乗誤差の場合、
$$\mathcal{L}(\hat{y},y) = \frac{1}{2}(\sigma(\mathbf{x}^\mathrm{T}\mathbf{w} )-y)^2$$
ここで,
$$u = \sigma(\mathbf{x}^\mathrm{T}\mathbf{w} ) -y$$
とすると、
$$\frac{\partial \mathcal{L}(u)}{\partial \mathbf{w}} = \frac{\partial \mathcal{L}(u)}{\partial u}\frac{\partial u}{\partial \mathbf{w}}$$


