線形時間によるソーティングアルゴリズム

最速のソートと言われているクイックソート、ヒープソート、マージソートなどの時間計算量は$\Theta(n\log n)$ですが、空間計算量をトレードして線形時間に落とすことができるアルゴリズムを実装していきます。

Pseudocode

countingSort(A,k)
    let out[1…A.len] 
    let countt[1…k]
    for i = i to k
        count[i] = 0
    for j = 1 to A.len  
        count[A[j]] += 1
    for i =2 to k
        count[i] += count[i-1]
    for j = A.len -> 1
        key = A[j]
        index = count[key]
        out[index] = key
        count[key] -= 1
    return out

Pythonで実装

上記のコードを利用して、Pyhonで実装してみます。

def counting_sort(A:list) -> list:
    nums = [i for i in range(max(A)+1)]
    count = {i:0 for i in nums}
    out = [0 for _ in range(len(A))]
    for i in A:
            count[i] += 1
    for i in range(1,len(nums)):
        count[nums[i]] += count[nums[i-1]]
    for j in range(len(A)-1,-1,-1):
        key = A[j]
        index = count[key]
        count[key] -= 1
        out[index-1] = A[j]
    return out

マージソートとの比較

マージソートを同じくPythonで実装して、要素数nについてのソート時間を比較してみます。

マージソートの実装

def merge(left:list,right:list) -> list:
    l_i:int = 0
    r_i:int = 0
    i:int = 0
    A:list = [0 for i in range(len(left) + len(right))]
    while l_i < len(left) and r_i < len(right):
        if left[l_i] < right[r_i]:
            A[i] = left[l_i]
            l_i += 1
        else:
            A[i] = right[r_i]
            r_i += 1
        i += 1
    while len(right) - r_i >= 1:
        A[i] = right[r_i]
        r_i += 1
        i += 1
    while len(left) - l_i >= 1:
        A[i] = left[l_i]
        l_i += 1
        i += 1
    return A 
def merge_sort(array:list) -> list:
    if len(array) <=1:
        return array
    mid:int = len(array)//2
    left:list = array[:mid]
    right:list = array[mid:]
    return merge(merge_sort(left),merge_sort(right))

実行時間の比較

nを増やしていき、それぞれのソートにかかった時間をプロットしていきいます。

import time 
import matplotlib.pyplot as plt 
fig = plt.figure()
I,ts_merge,ts_counting = [],[],[]

for i in range(1,100000,400):
    A = [i for i in range(i,0,-1)]
    dst = A[::-1]
    t_0 = time.time()
    m = merge_sort(A)
    t_merge = time.time() - t_0
    t_0 = time.time()
    c = counting_sort(A)
    t_counting = time.time() - t_0
    I.append(i)
    ts_merge.append(t_merge)
    ts_counting.append(t_counting)
    print(i)

plt.scatter(I,ts_merge,s=3,color = "black",label = "Merge Sort")
plt.scatter(I,ts_counting,s=3,color = "red",label = "Counting sort")
plt.grid()
plt.legend()
plt.xlabel('n')
plt.ylabel('time (ms)')
fig.savefig("a.png",dpi = 500)

実行結果

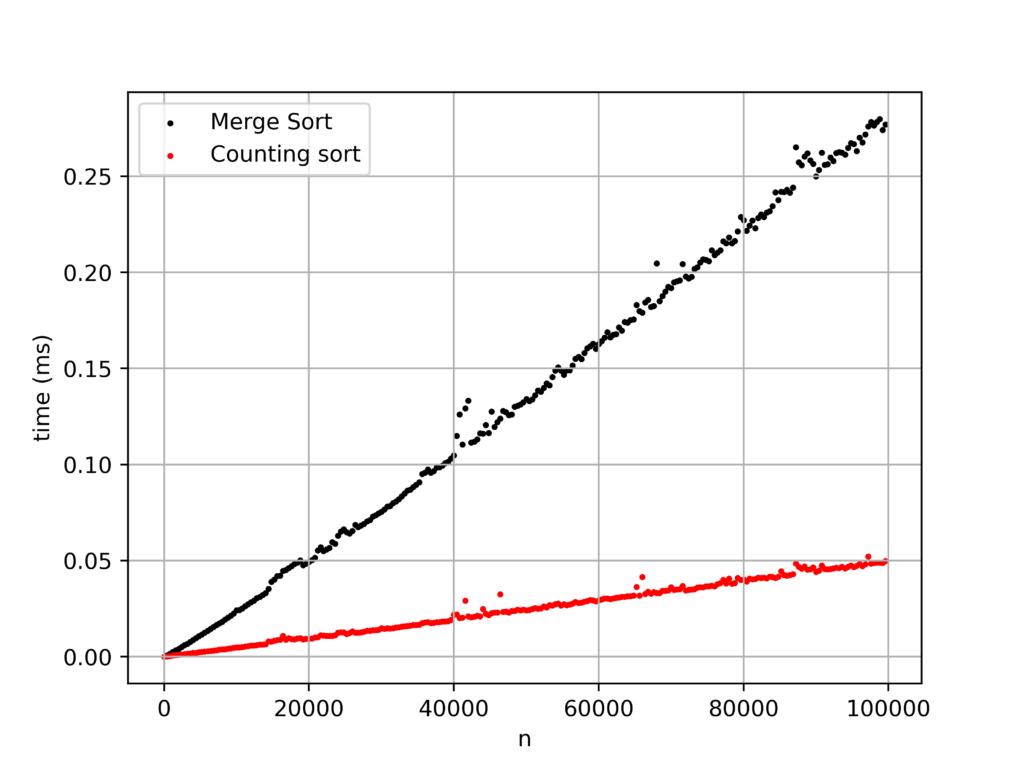
Counting sortの方が高速にソートできていることがわかります。

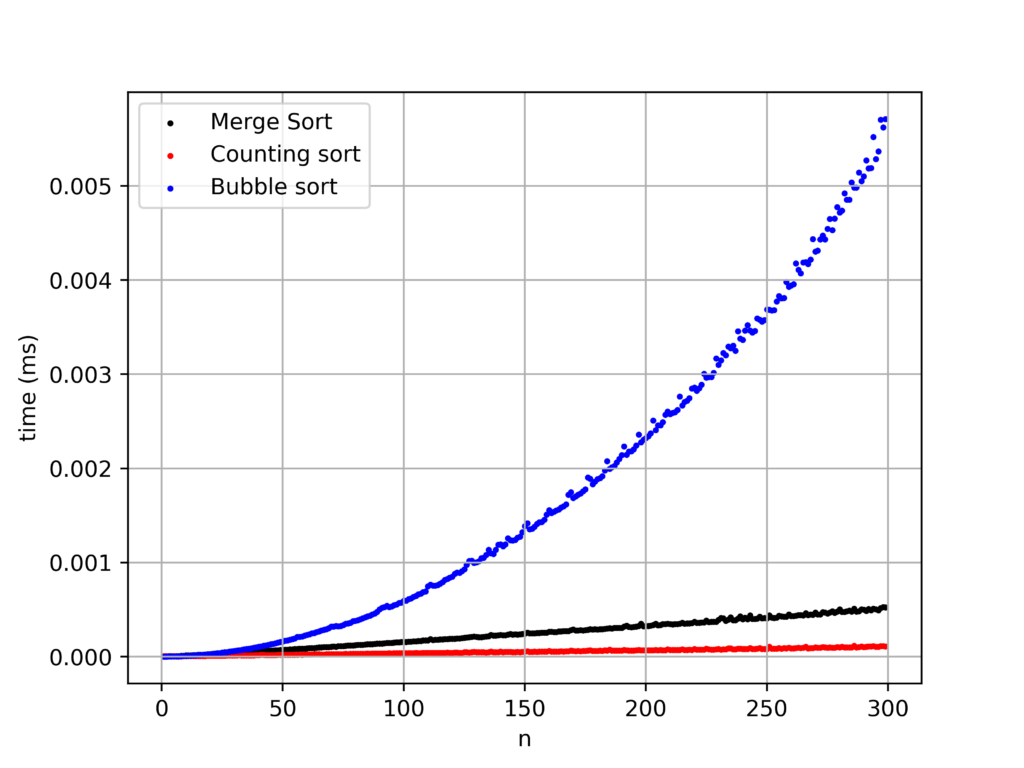
Bubble sort とも比較

計算量が$O(n^2)$になるソートとも比較してみます。

def merge(left:list,right:list) -> list:
    l_i:int = 0
    r_i:int = 0
    i:int = 0
    A:list = [0 for i in range(len(left) + len(right))]
    while l_i < len(left) and r_i < len(right):
        if left[l_i] < right[r_i]:
            A[i] = left[l_i]
            l_i += 1
        else:
            A[i] = right[r_i]
            r_i += 1
        i += 1
    while len(right) - r_i >= 1:
        A[i] = right[r_i]
        r_i += 1
        i += 1
    while len(left) - l_i >= 1:
        A[i] = left[l_i]
        l_i += 1
        i += 1
    return A 

def merge_sort(array:list) -> list:
    if len(array) <=1:
        return array
    mid:int = len(array)//2
    left:list = array[:mid]
    right:list = array[mid:]
    return merge(merge_sort(left),merge_sort(right))
def counting_sort(A:list) -> list:
    nums = [i for i in range(max(A)+1)]
    count = {i:0 for i in nums}
    out = [0 for _ in range(len(A))]
    for i in A:
            count[i] += 1
    for i in range(1,len(nums)):
        count[nums[i]] += count[nums[i-1]]
    for j in range(len(A)-1,-1,-1):
        key = A[j]
        index = count[key]
        count[key] -= 1
        out[index-1] = A[j]
    return out

def bubble_sort(seq):
    swapped = True
    while swapped:
        swapped = False
        for i in range(len(seq)-1):
            if seq[i]>seq[i+1]:
                seq[i],seq[i+1]=seq[i+1],seq[i]
                swapped = True
            else:
                pass
    return seq

import time 
import matplotlib.pyplot as plt 
fig = plt.figure()
I,ts_merge,ts_counting,ts_bubble = [],[],[],[]
for i in range(1,300,1):
    A = [i for i in range(i,0,-1)]
    dst = A[::-1]
    t_0 = time.time()
    m = merge_sort(A)
    t_merge = time.time() - t_0
    t_0 = time.time()
    c = counting_sort(A)
    t_counting = time.time() - t_0
    t_0 = time.time()
    b = bubble_sort(A)
    t_bubble = time.time() - t_0
    I.append(i)
    ts_merge.append(t_merge)
    ts_counting.append(t_counting)
    ts_bubble.append(t_bubble)
    print(i)

plt.scatter(I,ts_merge,s=3,color = "black",label = "Merge Sort")
plt.scatter(I,ts_counting,s=3,color = "red",label = "Counting sort")
plt.scatter(I,ts_bubble,s=3,color = "blue",label = "Bubble sort")
plt.grid()
plt.legend()
plt.xlabel('n')
plt.ylabel('time (ms)')
fig.savefig("a.png",dpi = 500)

実行結果