目次
直交射影行列の求め方
$A^\mathrm{T}A$が正則の元、直交射影行列$P$は以下のように定義される。
$$P = A(A^\mathrm{T}A)^{-1}A^\mathrm{T}$$
この時、
$$P^2=P$$
KerAとCoimgAの直交射影行列
以下の行列$M$について考える。
$$M=\begin {pmatrix}1&-1&2&-2\\0&1&-2&1\\1&0&0&-1\end{pmatrix}$$
この時、
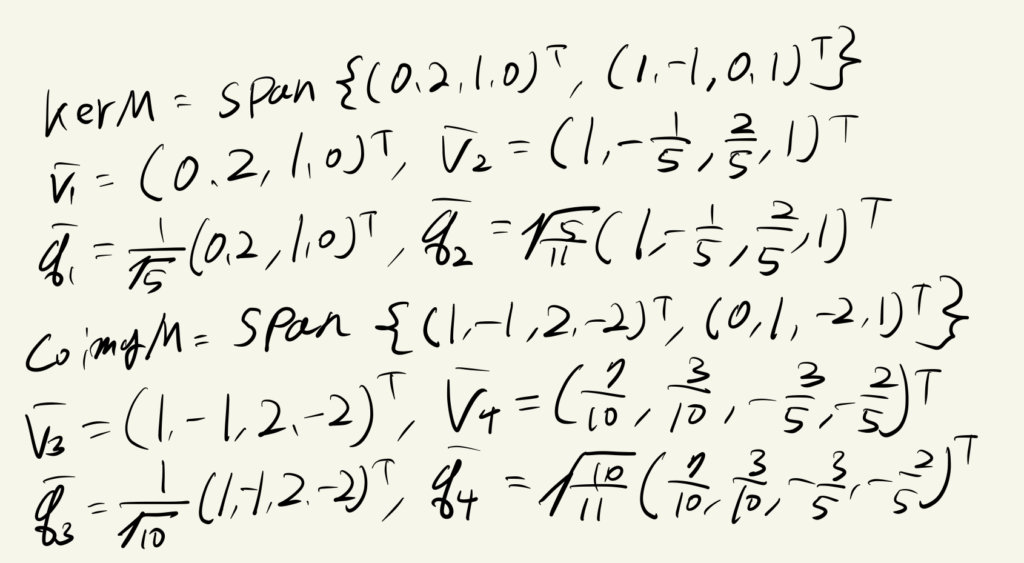
KerMの直交射影行列(1)
カーネルの基底を列ベクトルとして、
$$A=\begin {pmatrix}0&1\\2&-1\\1&0\\0&1\end{pmatrix}$$
とする。
この時、
$$A^\mathrm{T}A=\begin {pmatrix}5&-2\\-2&3\end{pmatrix}$$
$$(A^\mathrm{T}A)^{-1}=\frac{1}{11}\begin {pmatrix}3&2\\2&5\end{pmatrix}$$
よって、
$$P_{KerM} = \frac{1}{11}A\begin {pmatrix}5&-2\\-2&3\end{pmatrix}A^\mathrm{T}$$
計算すると、
$$P_{KerM}=\frac{1}{11}\begin {pmatrix}5&-1&2&5\\-1&9&4&-1\\2&4&3&2\\5&-1&2&5\end{pmatrix}$$
KerMの直交射影行列(2)
別の方法として、KerMの直交射影行列は以下のように定義できる。
$$P_{KerM} = (\mathbf{\bar{q_1}},\mathbf{\bar{q_2}})\begin {pmatrix}\mathbf{\bar{q_1}}^\mathrm{T}\\\mathbf{\bar{q_2}}^\mathrm{T}\end{pmatrix}$$
CoimgMの直交射影行列(1)
コイメージの基底を列ベクトルとして、
$$A=\begin {pmatrix}1&0\\-1&1\\2&-2\\-2&1\end{pmatrix}$$
この時、
$$A^\mathrm{T}A=\begin {pmatrix}10&-7\\-7&6\end{pmatrix}$$
$$(A^\mathrm{T}A)^{-1}=\frac{1}{11}\begin {pmatrix}6&7\\7&10\end{pmatrix}$$
よって、
$$P_{CoimgM} = \frac{1}{11}A\begin {pmatrix}6&7\\7&10\end{pmatrix}A^\mathrm{T}$$
計算すると、
$$P_{KerM}=\frac{1}{11}\begin {pmatrix}6&1&-2&-5\\1&2&-4&-1\\-2&-4&8&-2\\-5&1&-2&6\end{pmatrix}$$
CoimgMの直交射影行列(2)
$$P_{CoingM} = (\mathbf{\bar{q_3}},\mathbf{\bar{q_4}})\begin {pmatrix}\mathbf{\bar{q_3}}^\mathrm{T}\\\mathbf{\bar{q_4}}^\mathrm{T}\end{pmatrix}$$
KerMとCoimgMのコンポーネントと直交射影行列
$\bar{w} =(2,1,1,0)^\mathrm{T} $とすると,
$\mathbf{\bar{w}} = c_1\bar{\mathbf{q_1}}+ c_2\bar{\mathbf{q_2}}+ c_3\bar{\mathbf{q_3}}+ c_4\bar{\mathbf{q_4}}\:\: where \:\:\:c_i=\mathbf{\bar{q_i}} \cdot \mathbf{\bar{w}} \in \mathbb{R}^4$
この時、
$P_{KerM}\mathbf{\bar{w}} =c_1\bar{\mathbf{q_1}}+ c_2\bar{\mathbf{q_2}}$
$P_{CoimgM}\mathbf{\bar{w}} =c_3\bar{\mathbf{q_3}}+ c_4\bar{\mathbf{q_4}}$
よって、
$\mathbf{\bar{w}} = P_{KerM}\mathbf{\bar{w}} + P_{CoimgM}\mathbf{\bar{w}} $
また、
$P_{KerM} + P_{CoimgM} = \mathbf{E_4} $
Numpyで数値計算
import numpy as np
#KerM Orthogonal Projection P1
A = np.array([[0,1],[2,-1],[1,0],[0,1]])
A_t = np.transpose(A)
K = np.linalg.inv(A_t@A)
w =np.array([2,1,1,0])
P1 = A@K@A_t
print(P1@w)
print(P1)
#CoimgM Orthogonal Projection P2
A_2 = np.array([[1,0],[-1,1],[2,-2],[-2,1]])
A_2_t = np.transpose(A_2)
K_2 = np.linalg.inv(A_2_t@A_2)
P2 = A_2@K_2@A_2_t
print(P2@w)
print(P2)
print(P1+P2)
>>>
[1. 1. 1. 1.]
[[ 0.45454545 -0.09090909 0.18181818 0.45454545]
[-0.09090909 0.81818182 0.36363636 -0.09090909]
[ 0.18181818 0.36363636 0.27272727 0.18181818]
[ 0.45454545 -0.09090909 0.18181818 0.45454545]]
[ 1.00000000e+00 1.11022302e-16 -2.22044605e-16 -1.00000000e+00]
[[ 0.54545455 0.09090909 -0.18181818 -0.45454545]
[ 0.09090909 0.18181818 -0.36363636 0.09090909]
[-0.18181818 -0.36363636 0.72727273 -0.18181818]
[-0.45454545 0.09090909 -0.18181818 0.54545455]]
[[ 1.00000000e+00 5.55111512e-17 -5.55111512e-17 -2.77555756e-16]
[ 5.55111512e-17 1.00000000e+00 1.66533454e-16 -5.55111512e-17]
[-5.55111512e-17 1.66533454e-16 1.00000000e+00 1.66533454e-16]
[-2.77555756e-16 -5.55111512e-17 1.66533454e-16 1.00000000e+00]]



