集合から要素を定数時間で探索できるデータ構造について考えます。(高速化のためJavaを使用。)
今回は、Str型変数を引数としたハッシュ関数を使用して、配列のインデックスを返すという場合について考えます。
目次
ハッシュ関数評価方法
ハッシュ関数の評価方法は色々あると思いますが、今回はチェイン法で一旦全ての要素をハッシュテーブルに格納してから、その後に衝突回数を計測していきます。
ノードの作成
衝突が起こった際に値を同じインデックスに接続するためのノードを作成します。
public class Node<T extends Comparable<T>> {
private T data;
private Node<T> next;
public Node(T data) {
this.data = data;
this.next = null;
}
public T getData() {
return data;
}
public void setData(T data) {
this.data = data;
}
public Node<T> getNext() {
return next;
}
public void setNext(Node<T> next) {
this.next = next;
}
}文字列の読み込みクラス
約30万単語が記載されたテキストファイルを文字列の配列として取得します。ついでに結果を書き込めるようにもしておきます。
import java.io.*;
public class fileio {
String inputFilename;
String outputFilename;
public fileio(){
this.inputFilename = "input";
this.outputFilename = "out.txt";
}
public void setInputFilename(String inputFilename){
this.inputFilename = inputFilename;
}
public String[] readLines(){
File file = new File(this.inputFilename);
try{
BufferedReader br = new BufferedReader(new FileReader(file));
String s = br.readLine();
int i = 1;
while(s != null){
i++;
s = br.readLine();
}
s = br.readLine();
BufferedReader br2 = new BufferedReader(new FileReader(file));
String[] arr = new String[i-1];
for (int j = 0; j < i-1; j++) {
s = br2.readLine();
arr[j] = s;
}
br.close();
return arr;
}catch (Exception e){
return new String[0];
}
}
public void writeLines(String[] arr){
File fout = new File(this.outputFilename);
try{
FileOutputStream fos = new FileOutputStream(fout);
BufferedWriter bw = new BufferedWriter(new OutputStreamWriter(fos));
for (int i = 0; i < arr.length; i++) {
bw.write(arr[i] + "\n");
}
bw.close();
}catch (Exception e){
System.out.println(e);
}
}
}衝突検証クラス
このクラスに任意のハッシュ関数も含めるようにしました。
ハッシュ関数によって生成されたインデックスにノードを格納していき、各インデックスの鎖の長さをテキストとして出力します。
public class HashMap{
String[] scrabbleTxt = null;
Node<String>[] hashMap;
int tableSize;
public HashMap(String filename){
fileio fio = new fileio();
fio.setInputFilename(filename);
this.scrabbleTxt = fio.readLines();
this.tableSize =scrabbleTxt.length;
this.hashMap = new Node[this.tableSize];
}
public void outputText(String[] outStrings){
fileio fio = new fileio();
fio.writeLines(outStrings);
}
public static int hashFunc(String inputStr,int tableSize){
int h = 0;
for (int i = 0;i < inputStr.length();i++){
h += (inputStr).charAt(i);
}
return h%tableSize;
}
public static void main(String[] args) {
HashMap hmap = new HashMap("scrabble.txt");
int index;
for (int i = 0; i < hmap.scrabbleTxt.length; i++) {
index = hashFunc(hmap.scrabbleTxt[i], hmap.tableSize);
if (hmap.hashMap[index] == null){
hmap.hashMap[index] = new Node<String>(hmap.scrabbleTxt[i]);
}else{
Node<String> tmpNode = hmap.hashMap[index];
while (tmpNode.getNext() != null){
tmpNode = tmpNode.getNext();
}
tmpNode.setNext(new Node<String>(hmap.scrabbleTxt[i]));
}
}
String[] outStrings = new String[hmap.tableSize];
for (int i = 0; i < hmap.scrabbleTxt.length; i++){
if (hmap.hashMap[i] == null){
outStrings[i] = "0";
}else{
Node<String> tempNode = hmap.hashMap[i];
int n = 0;
while(tempNode.getNext() != null){
tempNode = tempNode.getNext();
++n ;
}
outStrings[i] = n + "";
}
}
hmap.outputText(outStrings);
System.out.println("Done");
}
}Pythonで可視化
javaから渡されたファイルを読み込んで、グラフ化します。
import matplotlib.pyplot as plt
fig = plt.figure()
with open("out.txt") as fp:
chain_i = [int(i.replace("\n","")) for i in fp.readlines()]
i = [i for i in range(len(chain_i))]
plt.scatter(i,chain_i,s=3,color = "gray")
plt.grid()
plt.xlabel("index")
plt.ylabel("Num of chain")
fig.savefig("chain.png",dpi=500)ハッシュ関数
ようやく検証用の体制が整ったので、いくつかハッシュ関数を作成して分析してみます。
一般的に、山が低く、散らばりが均一となるハッシュ関数が好ましいです。
mod
この関数は上記の検証用にも実装しているシンプルなものです。
文字の全てのASCIIコードを加算して、modを求めるだけのハッシュ関数です。
public static int hashFunc(String inputStr,int tableSize){
int h = 0;
for (int i = 0;i < inputStr.length();i++){
h += (inputStr).charAt(i);
}
return h%tableSize;
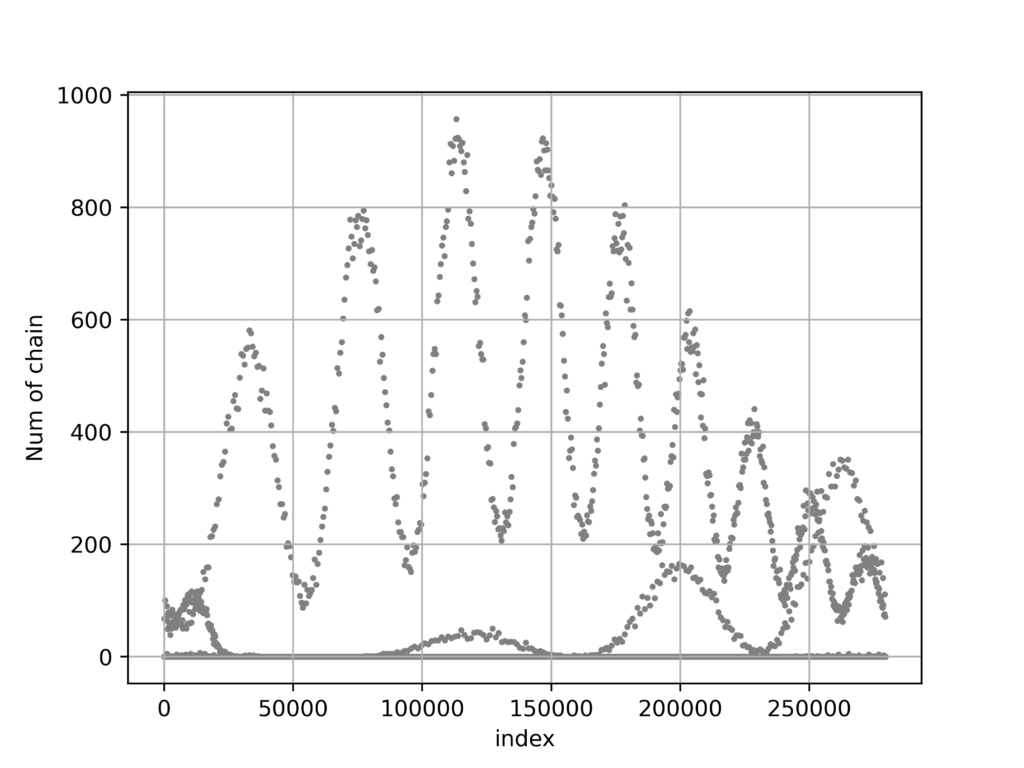
}実行結果
衝突が一部分に偏っていることがわかります。
ビットシフト演算
ビットシフト演算を使用してみます。
public static int hashFunc(String inputStr,int tableSize){
int h = 13;
for (int i = 0; i < (inputStr.toString()).length(); i++) {
char val = inputStr.toString().charAt(i);
int shift = ((i * h) % 4) * 7;
h ^= (int)val << shift;
}
if ( h % (tableSize) <=0){
return - h % (tableSize);
}
return h % (tableSize) ;
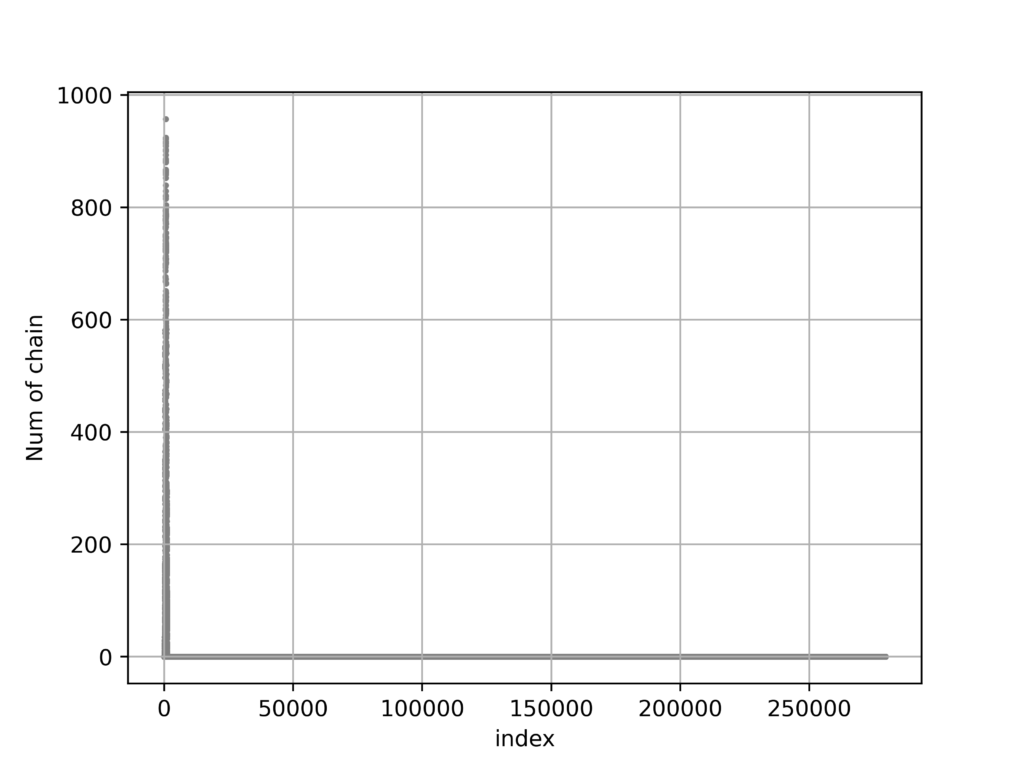
}実行結果
いい感じに拡散しています。
多重ビットシフト演算
ビットシフトを繰り返してみます。
public static int hashFunc(String inputStr,int tableSize){
int h = 113;
for (int i = 0; i < (inputStr.toString()).length(); i++) {
char val = inputStr.toString().charAt(i);
int shift = ((i * h) % 4) * 7;
h ^= (int)val << shift;
h += (int)val << shift;
h += (int)val << shift;
h ^= (int)val << shift;
}
if ( h % (tableSize) <=0){
return - h % (tableSize);
}
return h % (tableSize) ;
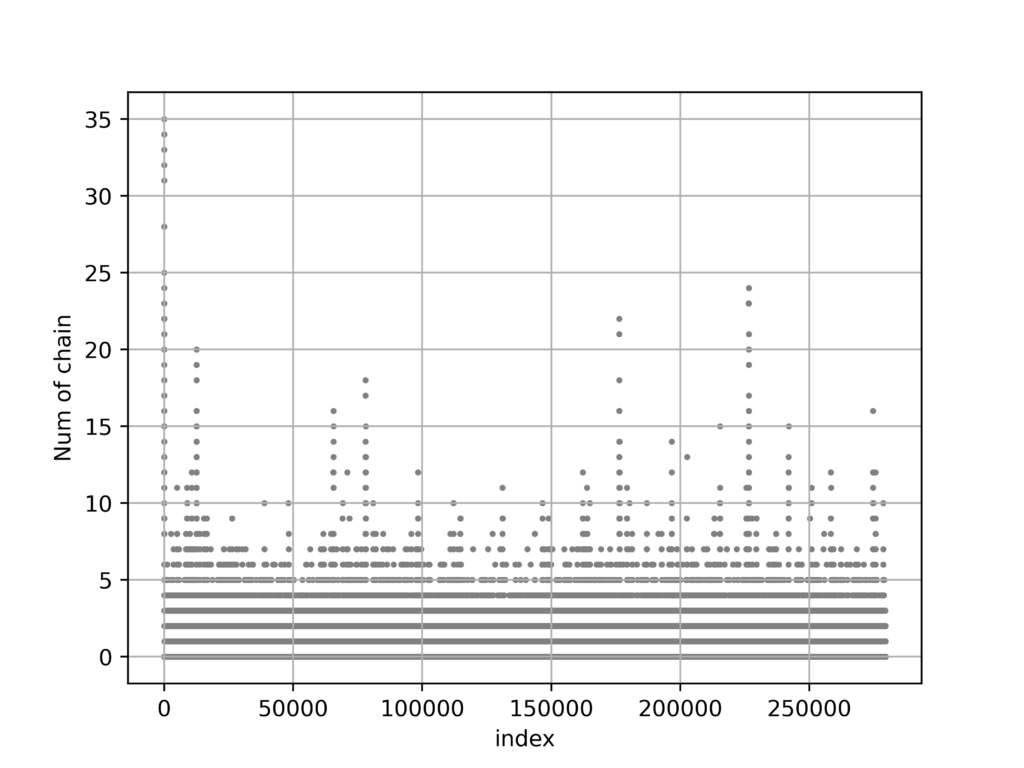
}実行結果
正弦関数
public static int hashFunc(String inputStr,int tableSize){
int h = 0;
for (int i = 0;i < inputStr.length();i++){
h += (inputStr).charAt(i);
}
return (int) Math.abs(Math.round(tableSize*Math.sin(h))%tableSize);
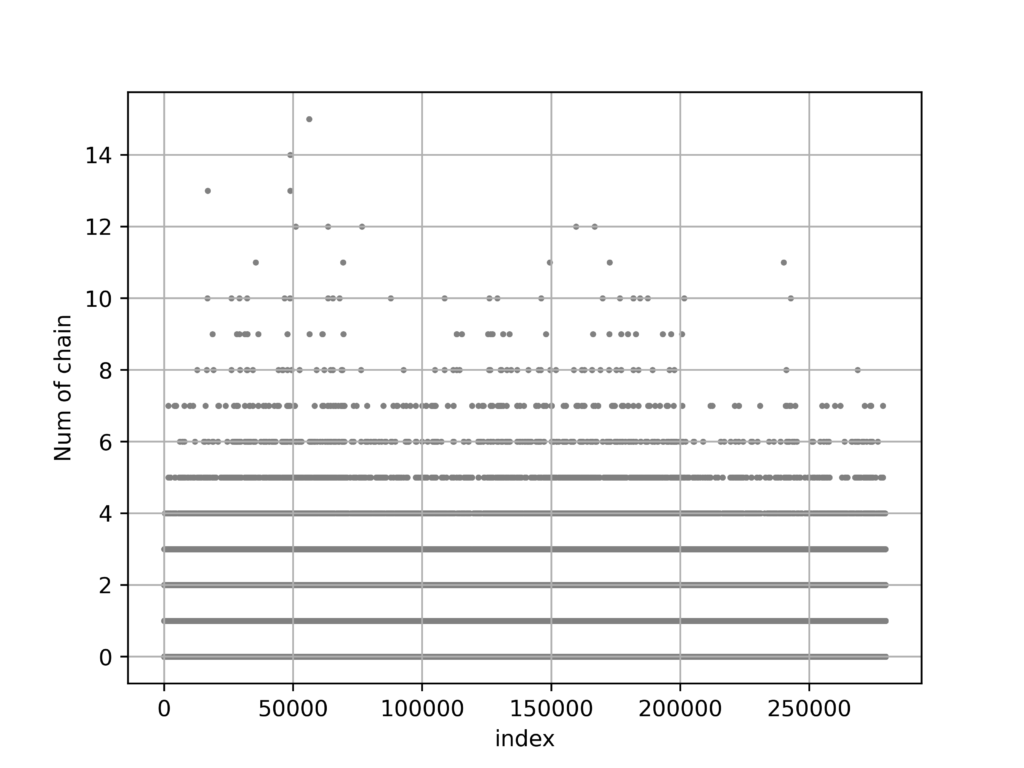
}実行結果
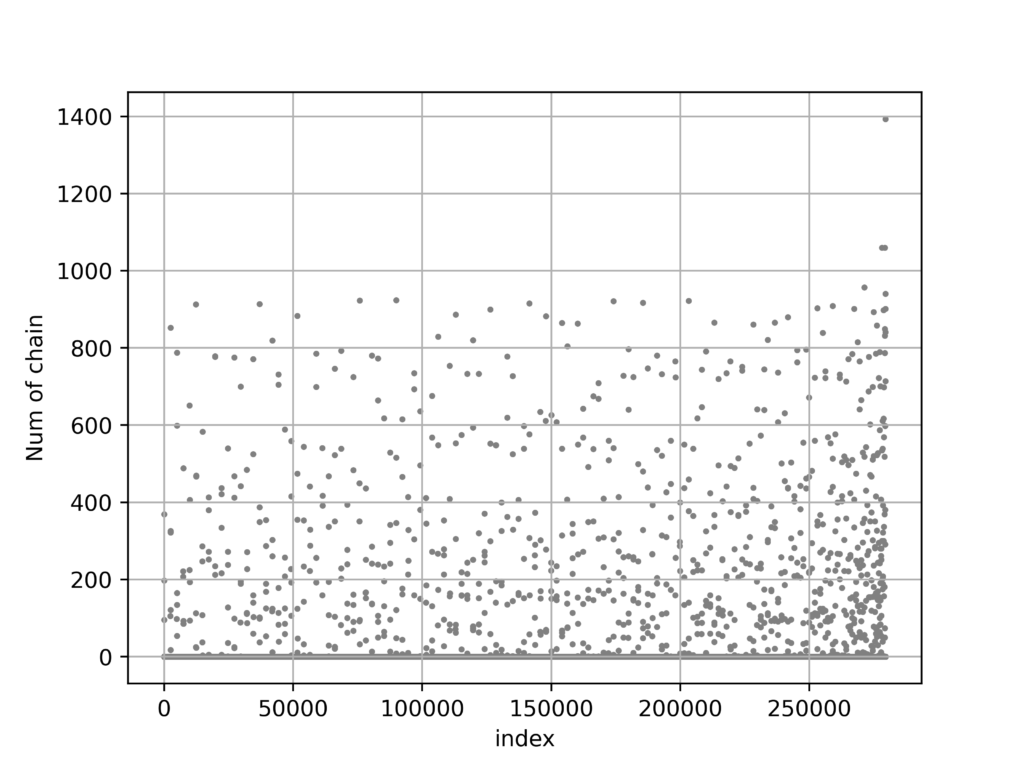
対数関数
public static int hashFunc(String inputStr,int tableSize){
int h = 0;
for (int i = 0;i < inputStr.length();i++){
h += (inputStr).charAt(i);
}
return (int) Math.abs(Math.round(tableSize*Math.log(h))%tableSize);
}実行結果