今となれば、DNAに突然変異等のランダムな変異が入ることにより生物が進化して、その進化後の個体の中で環境に適したものが生き残りやすいという理論は簡単に受け入れることができますが、昔の人たちは今回紹介する一段階淘汰論を本気で信じていたかもしれません。
今回は、そんな一段階淘汰と累積淘汰によるターゲット塩基配列の生成コストを検証してみます。
目次
一段階淘汰
名前の通り、一段階で配列を生成し、環境に適応した配列(ターゲット配列)以外を排除します。自然界では、複数パターンが環境に適応できますが、今回のシミュレーションではただ一つの塩基配列を使用して一段階淘汰にかかるコストを計算します。
もちろん、一段階淘汰の場合選び方と並べ方の問題なので、1ヌクレオチド増えるごとに文字通り桁違いのコストになりますが、練習がてらアルゴリズムを構築してみます。
アルゴリズム
1.n桁のターゲット塩基配列を生成。
2.同様にn桁のランダムな塩基配列を生成し、
実装
nが10を超えたあたりから明らかにコストが急増するのが目に見えているため、今回はn=10までを検証してみます。
import random
import matplotlib.pyplot as plt
class Seq:
def __init__(self,n) -> None:
self.nucleotides = ['A','C','G','T']
self.length = n
def set_seq(self):
seq = ''
for i in range(self.length):
seq += random.choice(self.nucleotides)
return seq
fig = plt.figure()
plt.grid()
plt.xlabel('bps')
plt.ylabel('Gen_n')
for k in range(10):
seq = Seq(k+1).set_seq()
i = 0
while True:
i+=1
if seq ==Seq(k+1).set_seq():
gen = i
break
else:
pass
plt.scatter(k+1,i)
fig.savefig('result.png',dpi=500)実行結果
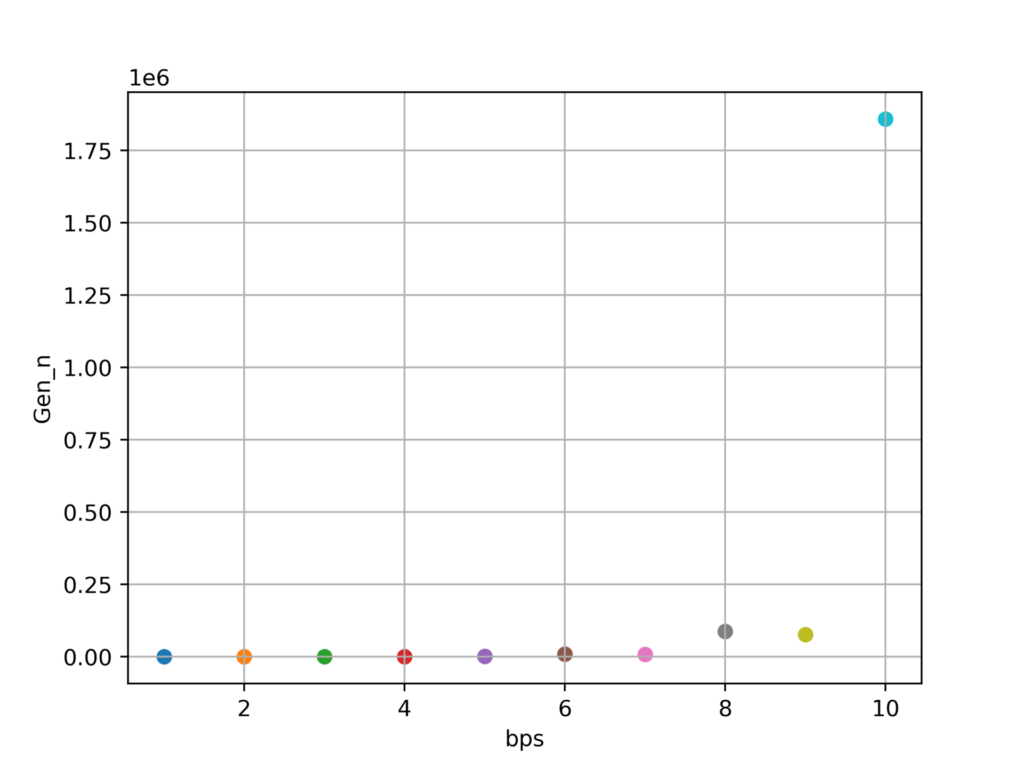
塩基数が10の時点で生成コストが百万を超えています。
累積淘汰
一世代淘汰に対して、累積淘汰では前世代で”最良”、つまり一番ターゲットに近かったスコアを出した配列を次世代の初期配列とすることができるメリットがあります。
アルゴリズム
1.n桁のターゲット配列Aを生成する。
2.同様にn桁の配列Bをランダムに生成する。(ここまでは一段階淘汰と同じ。)
3.Bにm%の確率でランダム変異を加えた配列Ciをi個生成する。
4.AとCiを比較し、一致割合をスコアとする。一番スコアの高かった配列のみを保持し2へ戻る。
5.4の時点でスコアが1となれば操作を終了。5に達するまでに要した世代をスコアとする。
実装
一段階淘汰で生成コストが1000000を超えた塩基数10の配列を累積淘汰で生成してみます。なお、変異確率は3%、1世代での配列生成数は100とします。
import random
class Seq:
def __init__(self) -> None:
self.nucleotides = ['A','C','G','T']
self.chance_of_mutation = 0.03
self.seq_length = 10
def set_seq(self):
seq = ''
for i in range(self.seq_length):
seq += random.choice(self.nucleotides)
return seq
def mutate(self,seq):
new_seq = ''
for i in range(self.seq_length):
if random.random()<self.chance_of_mutation:
new_seq += random.choice(self.nucleotides)
else:
new_seq += seq[i]
return new_seq
def get_score(target,seq):
score = 0
for i in range(len(target)):
if target[i] == seq[i]:
score +=1
return score
target = Seq().set_seq()
seq = Seq().set_seq()
score, n= 0 ,0
while score != len(target):
n+=1
mutation_succeeded = False
for i in range(100):
mutant = Seq().mutate(seq)
if get_score(target,mutant)>score:
seq = mutant
score = get_score(target,mutant)
mutation_succeeded = True
if mutation_succeeded:
print('Gen{}:Score{}'.format(n,score/len(target)))実行結果
Gen1:Score0.8-CACGTGCTCT
Gen2:Score0.9-GACGTGCTCT
Gen6:Score1.0-GACGTGCTTT6世代でターゲット配列に到達していることがわかります。
次に同様のアルゴリズムで、塩基数10000の配列について実行してみます。
変異確率は0.01%に落とします。
import random
class Seq:
def __init__(self) -> None:
self.nucleotides = ['A','C','G','T']
self.chance_of_mutation = 0.03
self.seq_length = 10000
def set_seq(self):
seq = ''
for i in range(self.seq_length):
seq += random.choice(self.nucleotides)
return seq
def mutate(self,seq):
new_seq = ''
for i in range(self.seq_length):
if random.random()<self.chance_of_mutation:
new_seq += random.choice(self.nucleotides)
else:
new_seq += seq[i]
return new_seq実行結果
Gen4592:Score0.9982
Gen4667:Score0.9983
Gen4687:Score0.9984
Gen4845:Score0.9985
Gen4969:Score0.9986
Gen4973:Score0.9987
Gen4981:Score0.9988
Gen5094:Score0.9989
Gen5118:Score0.999
Gen5179:Score0.9991
Gen5189:Score0.9992
Gen5495:Score0.9993
Gen5591:Score0.9994
Gen5641:Score0.9995
Gen5703:Score0.9996
Gen5762:Score0.9997
Gen6051:Score0.9998
Gen6832:Score0.9999
Gen7113:Score1.0


