非接触温度測定

熱赤外線の放射エネルギー等を利用して物体の温度を算出する方法は非接触温度測定と呼ばれます。

今回は非接触温度測定に関して、いくつかの法則を見ていきます。

ステファン・ボルツマンの法則

法則の意味

黒体1㎠から毎秒放射するエネルギーはその絶対温度の４乗に比例する。

$$E=\sigma T^4$$

例えば、太陽の放射エネルギーをEとすれば、その表面温度Tは

$$T_{sun}=\sqrt[4]{\frac{E}{\sigma}}$$

となります。

ウィーンの変位則

法則の意味

物体の温度が高くなるにつれて放射される最大波長が短い方にシフトする。

$$\lambda_{max}T=C$$

式において、定数Cは2897 μmKとなります。

例えば、T(K)の物体が放射する最大波長は

$$\lambda_{max}=\frac{C}{T}$$

となります。

プランクの法則

プランクの法則において、黒体輻射による電磁波の単位面積、立体角、周波数あたりの分光放射輝度は以下のように、周波数と温度の二変数関数として表されます。

$$I(\nu,T)=\frac{2h{\nu}^3}{c^2}\frac{1}{e^{h\nu /kT}-1}$$

全立体角について積分すると

$$u(\nu,T)=\frac{8\pi h\nu^3}{c^3}\frac{1}{e^{h\nu /kT}-1}$$

左側の定数項を除いた以下の式について考えてみると、

$$f(\nu,T)=\frac{\nu^3}{e^{\nu /T}-1}$$

振動数、温度を軸にとったグラフを描いてみます。

import numpy as np 
import matplotlib.pyplot as plt 


fig = plt.figure()
ax = fig.add_subplot(111, projection='3d')
ax.set_xlabel(r"$\nu$", size = 14)
ax.set_ylabel("T", size = 14)
ax.set_zlabel(r"$F(\nu,T$)", size = 14)

T = np.linspace(10,5000,1000)
Nu = np.linspace(10,1000,1000)
T, Nu = np.meshgrid(T, Nu)
f_t = Nu**3/(np.exp(Nu/T)-1)
ax.plot_surface(T, Nu, f_t, cmap = "plasma")
plt.show()
fig.savefig('result.png',dpi=500)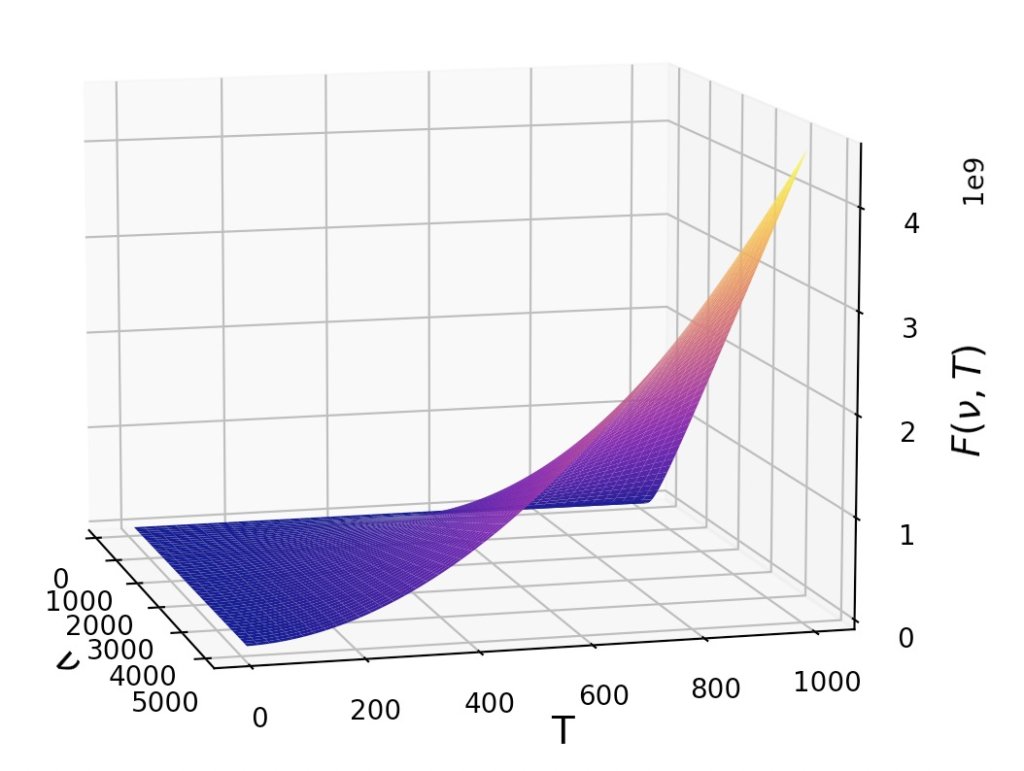

ピーク周波数を求めるために、振動数について偏微分すると

$$\begin{align}\frac{\partial}{\partial \nu}f(\nu,T)&=\frac{\partial}{\partial \nu}\frac{\nu^3}{e^{\nu /T}-1}\\&=\frac{\nu^2(3e^{\frac{\nu}{T}}-\frac{\nu}{T} e^{\frac{\nu}{T}}-3)}{(e^{\nu/T}-1)^2}\end{align}$$

ここで、ピーク位置（変曲点）において

$$\frac{\partial}{\partial \nu}f(\nu,T)=0$$

であるから、

$$3e^{\frac{\nu}{T}}-\frac{\nu}{T} e^{\frac{\nu}{T}}=3$$

$$t=\frac{\nu}{T}\quad \forall T >0$$

$$\therefore e^{-t}+\frac{t}{3}=1$$

ここで一つ問題が発生します。

上の式のtの値がわかりません。明らかに、t=0の時は成り立ちますが、振動数が０はあり得ないので、もう一つの解が存在するはずです。

ニュートン法による近似解

せっかくなので、ニュートン法によって近似解を出してみたいと思います。

まずは、上記の式を関数化します。

$$f(t)=e^{-t}+\frac{t}{3}-1$$

import numpy as np 
import matplotlib.pyplot as plt 
fig = plt.figure()
plt.xlabel('t')
plt.ylabel('f(t)')
plt.grid()
plt.hlines(0,0,4,color='red')
t = np.linspace(0,4,10000)
f_t = np.exp(-t)+t/3-1
plt.plot(t,f_t)
fig.savefig('result_1.png',dpi=500)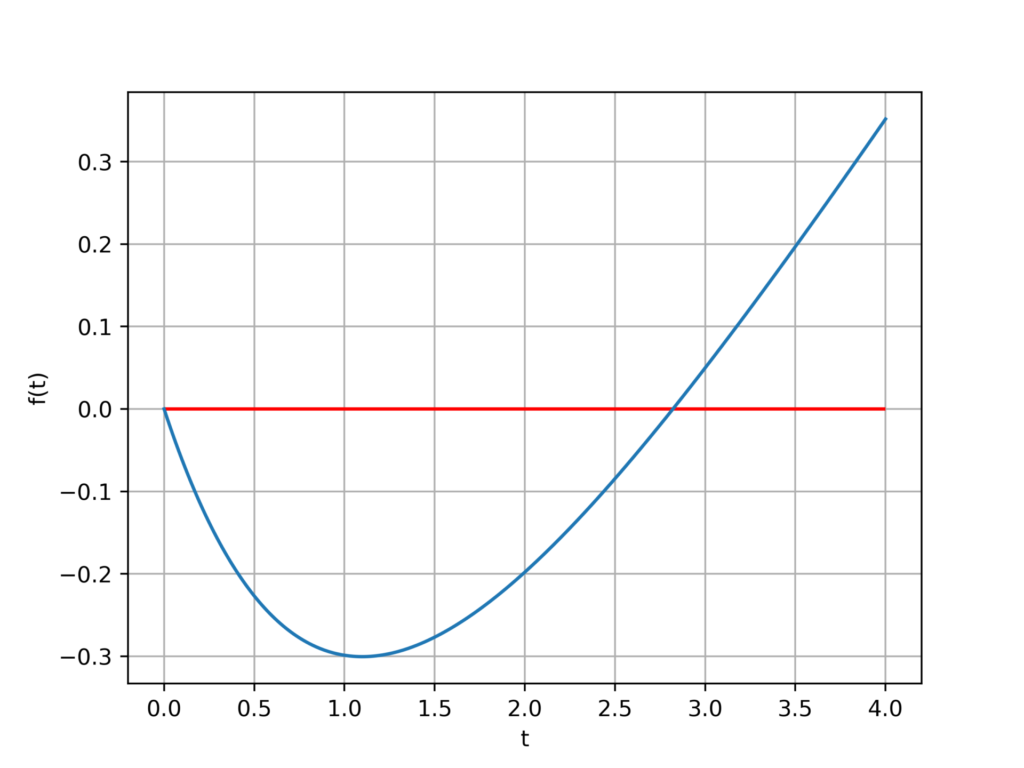

初期値を3に設定してニュートン法で計算してみます。

import numpy as np 

def N_R(t_i):
    f_ti=np.exp(-t_i)+t_i/3-1
    df_dt_i = -np.exp(-t_i)+1/3
    P_i = (t_i,f_ti)
    return -((P_i[1]-df_dt_i*P_i[0])/df_dt_i)
t_i = float(3)
for i in range(5):
    t_i = N_R(t_i)
    print(t_i)

>>>
2.8244128929932226
2.8214403305978797
2.8214393721221787
2.821439372122079
2.8214393721220783

早い段階から収束していることがわかります。

このことから

$$t\simeq 2.8214 \iff \nu_{max} \propto 2.8214T (\forall T>0)$$

が成り立つことがわかります。

ここで、波長と振動数の関係から、

$$\lambda_{max}\propto \frac{2.8214}{T}$$

が成り立ちます。

今回は、プランク定数などの定数項を省略して考えましたが、上式の定数が変わるだけで、プランクの法則からウィーンの法則と全く同じ関係が導出できていることがわかります。