正直、数学の「整数分野」はあんまり好きじゃないです。
素数とか聞いても魅力を感じないし、わざわざ考えようとも思いません。
ですが、せっかくなのでpythonでn番目の素数を簡単に求めるコードを考えてみたいと思います。
目次
素数の定義
初めに、簡単に素数について確認しておくと
素数:1とその数以外で割れない数
となります。
コード
これは至ってシンプルで、定義に従って書くだけです。
変数prime_nを判定用に使用しました。
def get_prime_number(n,m):
prime_number = []
for i in range(1,n):
prime_n = True
for j in range(2,i):
if i%j == 0:
prime_n = False
break
if prime_n:
prime_number.append(i)
return prime_number[m]第一因数に素数の探索範囲を、第二引数に何番目の素数かを指定する数を入れます。
実行時間について
せっかくなので、実行時間について、探索範囲が増えるとどれくらいの差があるのかをグラフにプロットしていってみたいと思います。
計測ように先程の関数を少し書き換えます。
import time
def get_prime_number(n):
start = time.time()
prime_number = []
for i in range(1,n):
prime_n = True
for j in range(2,i):
if i%j == 0:
prime_n = False
break
if prime_n:
prime_number.append(i)
process_time = time.time() - start
return process_time
今回はmatplotlibを利用し、各探索範囲xにかかる時間yを縦軸にプロットして行きます。
fig = plt.figure()
from tqdm import tqdm
x = [100*i for i in tqdm(range(100))]
y = [get_prime_number(x[i]) for i in tqdm(range(len(x)))]
plt.scatter(x,y)
plt.xlabel('x')
plt.ylabel('y')
plt.grid()
fig.savefig('img.jpg')結果は以下のようになります。
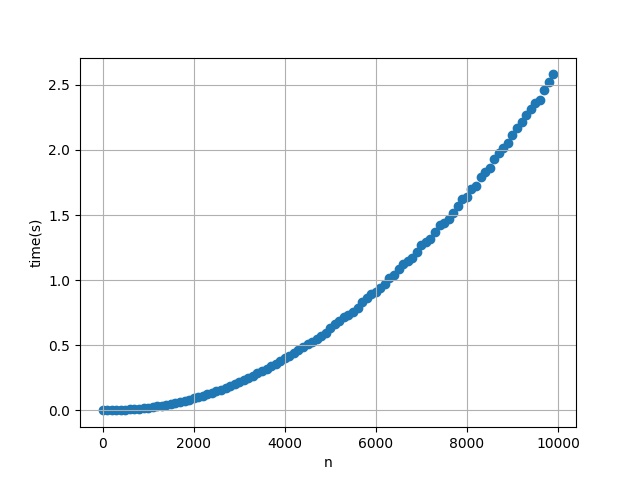
関数の計算量がO(N^2)になっているので当たり前ですね。
ついでに素数をプロット
素数をプロットしてみる。
fig = plt.figure()
x = get_prime_number(1000)
y = [i for i in range(len(x))]
plt.scatter(x,y,s=1,color ='red')
plt.xlabel('n')
plt.ylabel('prime_number')
plt.grid()
fig.savefig('img.jpg')こんな感じに、、、
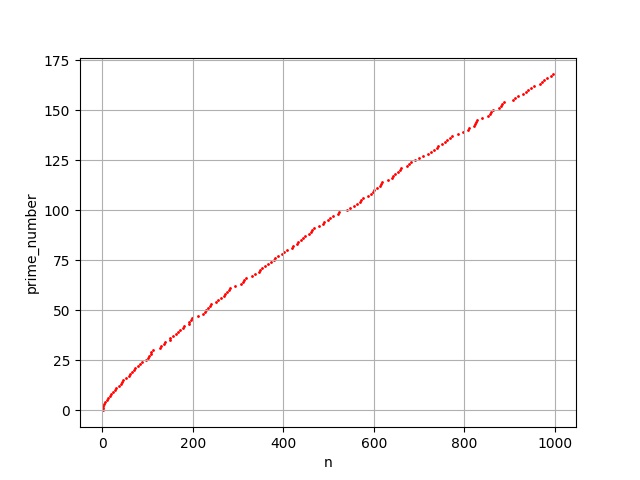
これを数億まで増やして、極めて精度の高い近似曲線を作ることができれば素数の一般項を求めることができるのかなと思ったりもしました。



