Pythonの組み込みソートアルゴリズムになんとかして勝つ

最速ソートと言われているクイックソートよりもさらに計算量を落としたカウンティングソートがありますが、pythonで実装したところ最適化された標準ソートにボロ負けでした。

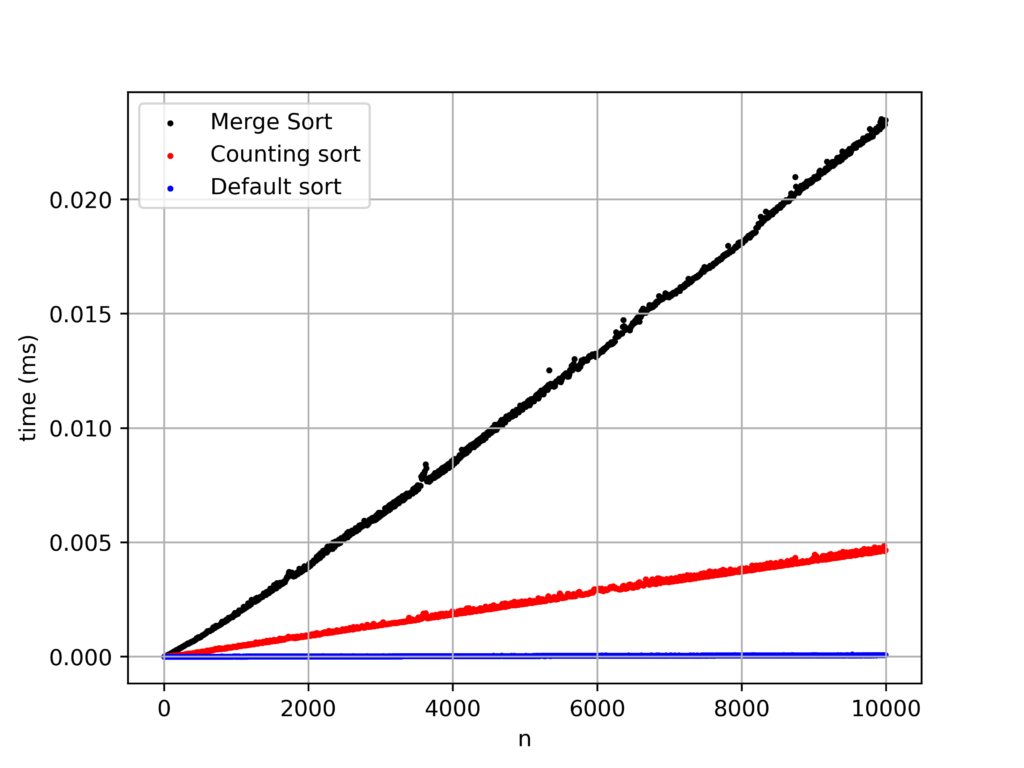
そのため、今回はPython標準ソートに勝てる条件を探っていきます。

カウントソート

標準ソートに大きく差をつけられていた従来のカウントソートアルゴリズムです。

def counting_sort(A:list) -> list:
    nums = [i for i in range(max(A)+1)]
    count = {i:0 for i in nums}
    out = [0 for _ in range(len(A))]
    for i in A:
            count[i] += 1
    for i in range(1,len(nums)):
        count[nums[i]] += count[nums[i-1]]
    for j in range(len(A)-1,-1,-1):
        key = A[j]
        index = count[key]
        count[key] -= 1
        out[index-1] = A[j]
    return out

最適化カウントソート

上記のアルゴリズムの無駄を省いて最適化します。

 def counting_sort_optimized(arr):
    max_ = max(arr)
    min_ = min(arr)
    count = [0] * (max_ - min_ + 1)
    for i in arr:
        count[i - min_] += 1
    return [I for i, c in enumerate(count, start=min_) for _ in range(c)]

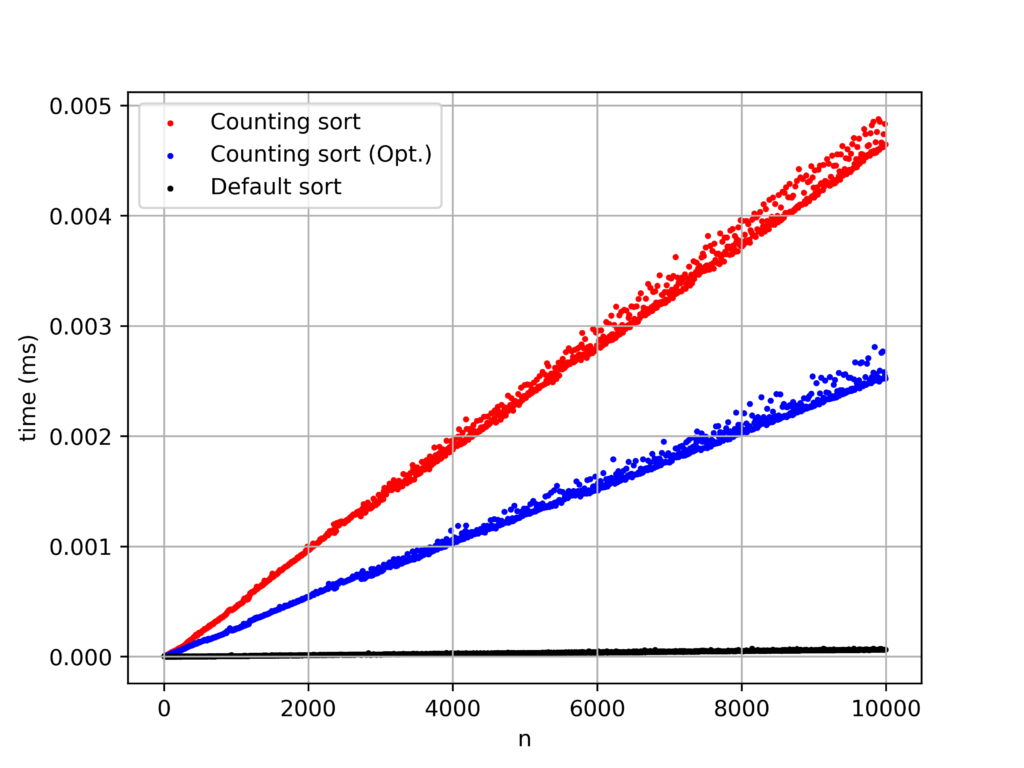
最適化後も組み込みアルゴリズムに届きません。

この原因として、ソート配列が単純すぎることが原因だと考えられるため、組み込みソートの弱点を探るべく、乱数を発生させて検証します。

ガウス分布に従う乱数

ガウス分布に従うように生成された乱数配列を使用してみます。

import time 
import matplotlib.pyplot as plt 
fig = plt.figure()
I,ts_countopt,ts_default,ts_count = [],[],[],[]
for i in range(1,300,1):
    A = [int(abs(np.random.normal(i,np.sqrt(i)))) for i in range(i,0,-1)]
    t_0 = time.time()
    c = counting_sort(A)
    t_counting = time.time() - t_0
    t_0 = time.time()
    c_opt = counting_sort_opt(A)
    t_copt = time.time() - t_0
    t_0 = time.time()
    s = sorted(A)
    t_default = time.time() - t_0
    I.append(i)
    ts_countopt.append(t_copt)
    ts_counting.append(t_counting)
    ts_default.append(t_default)
    print(i)

plt.scatter(I,ts_default,s=3,color = "black",label = "Default Sort")
plt.scatter(I,ts_counting,s=3,color = "red",label = "Counting sort")
plt.scatter(I,ts_countopt,s=3,color = "blue",label = "Counting sort (Opt.)")
plt.grid()
plt.legend()
plt.xlabel('n')
plt.ylabel('time (ms)')
fig.savefig("a.png",dpi = 500)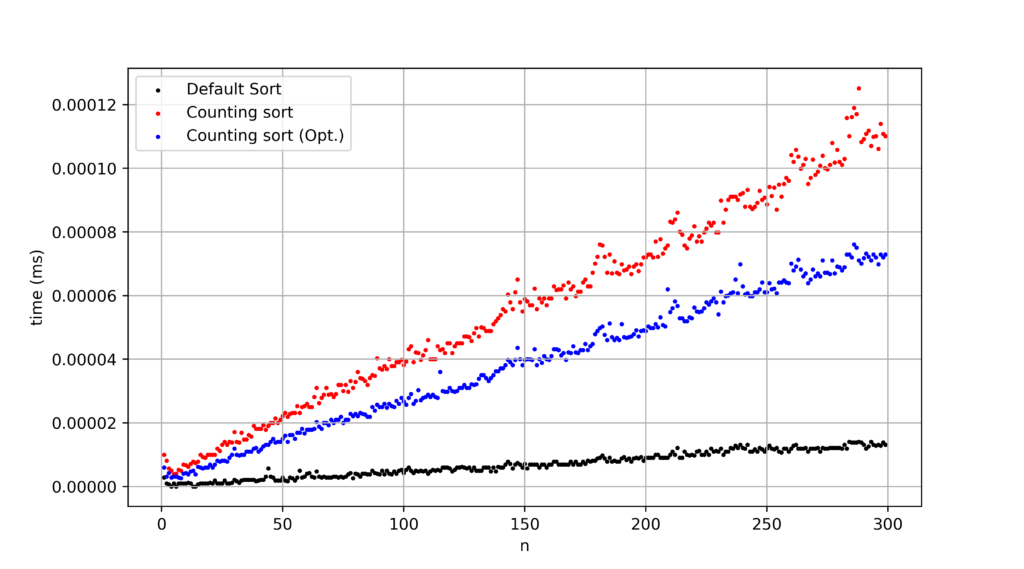

まだ組み込みアルゴリズムの方が安定しています。

二項分布

 A = [int(abs(np.random.binomial(10, 0.5))) for i in range(i,0,-1)]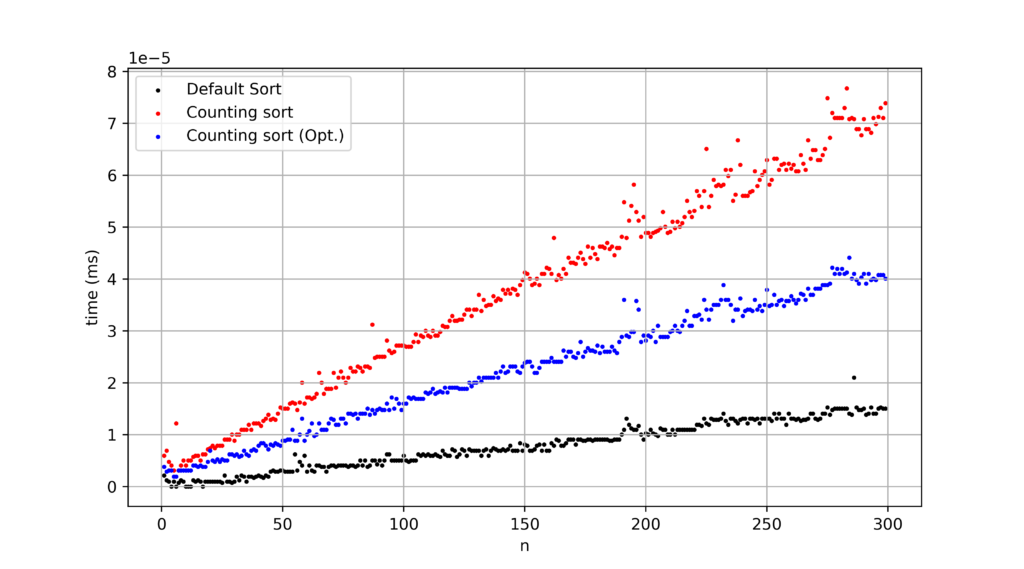

まだ負けてます。

ベータ分布

A = [int(abs(np.random.beta(1, i))*10000) for i in range(i,0,-1)]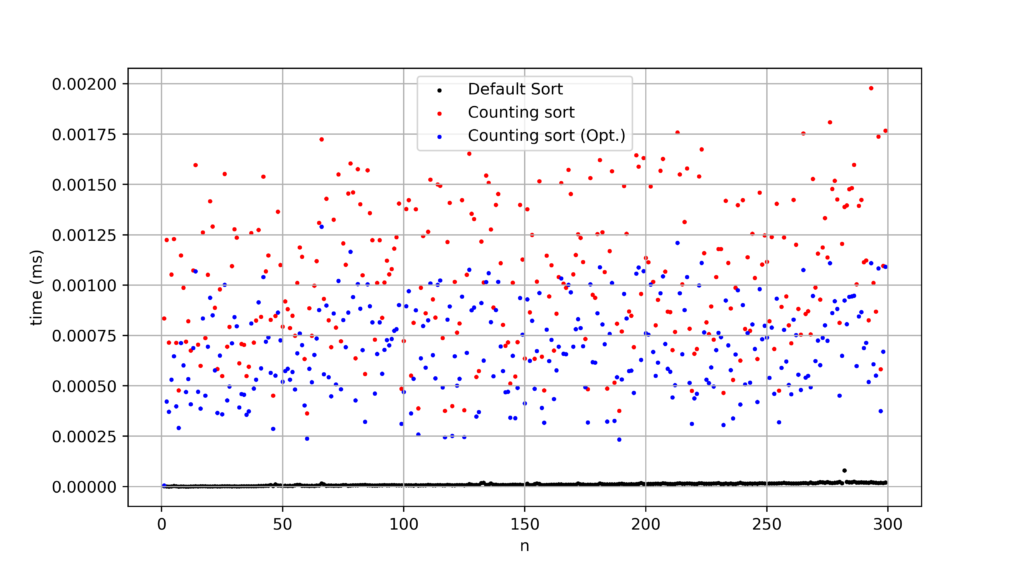

自家製アルゴリズムのみがキツくなってます。

ガンマ分布

 A = [int(abs(np.random.gamma(1, 10))*10000) for i in range(i,0,-1)]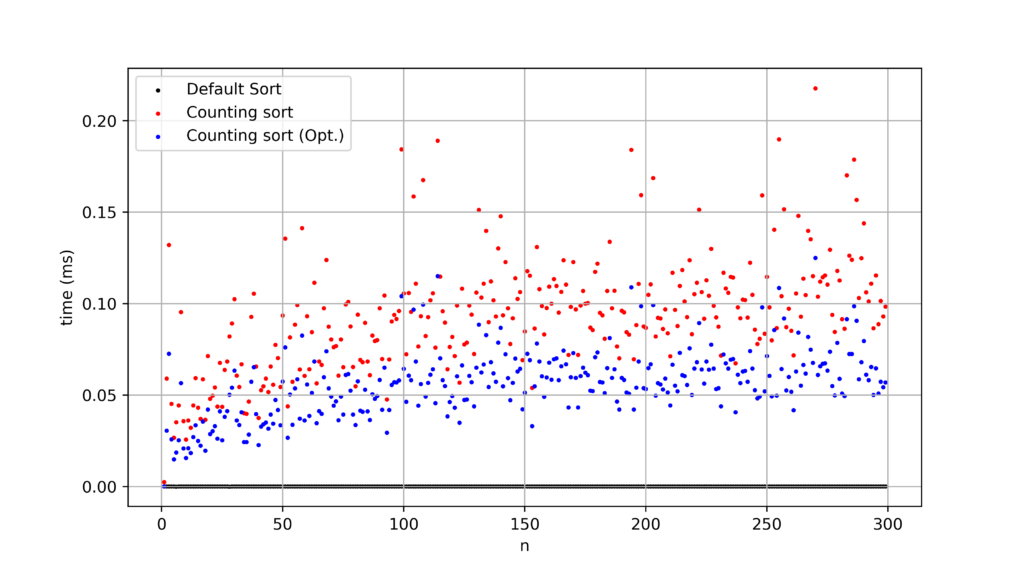

ほぼ平らです。

一様分布

A = [int(abs(np.random.randint(1,100))) for i in range(1000,0,-1)]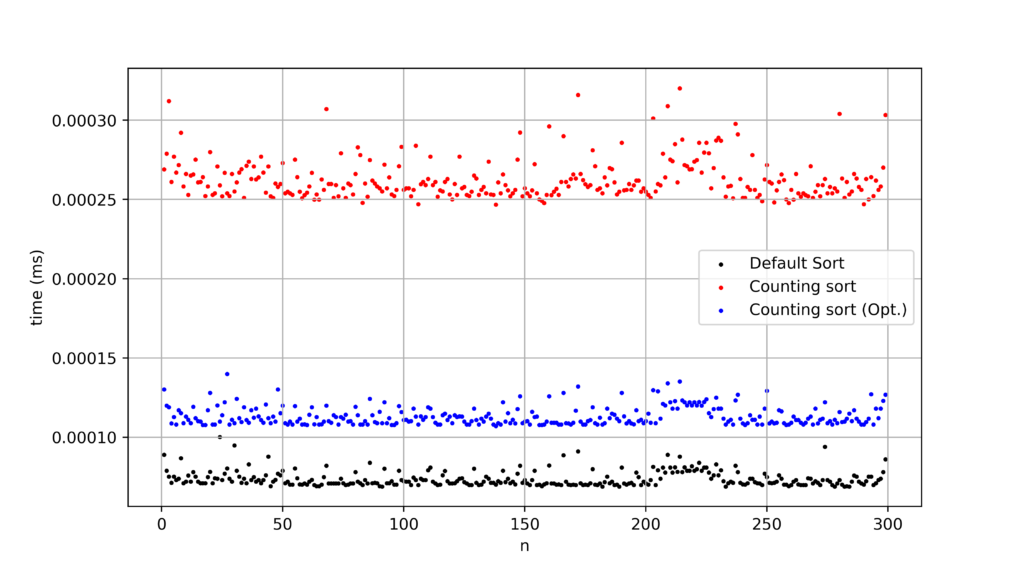

どうやっても勝てないので今度Javaで復讐します。