pythonでモンテカルロ法の実装

確率論を勉強しているときに、モンテカルロ法というものに出会ったので、一例としてpythonで実装してみたいと思います。

円周率の計算

モンテカルロ法の応用例のうち代表的なものとして、円周率の計算があります。

半径rの円に接する外接矩形(正方形）の面積Sは

$$S=4r^2$$

となり、この時の円の面積Aは当然

$$A=πr^2$$

となります。

この時、定数Kを用いて

$$K=A/S$$

とおけることから、

$$π=4K$$

という式を得ます。

ここで、上述の外接矩形内に無作為に点をプロットしていき、円の中に入った点の数と全プロット数の比を使用してKの値を近似することができます。

離散的な実装

シンプルにするために、pythonを用いて離散的な実装を行っていきます。

モジュールのインポート

今回は以下のモジュールを使用します。

import numpy as np 
import random
import matplotlib.pyplot as plt 
from tqdm import tqdm

numpyはarray出力用、randomは乱数生成用、matplotlibは計算結果のプロット用です。

tqdmモジュールは計算量が増えた時に残り時間を把握するために使用します。

内外判定用の関数

ランダムに生成した座標が円の内部にあるかどうかを以下のように判定します。

def is_within(x,y,radius,p,q):
    if ((x-p)**2 + (y-q)**2)< radius**2:
        return True

引数p,qには円の中心座標を入力します。

座標情報の落とし込み

numpy zerosを使用して、2048×2048の配列を生成します。また、arrayから、半径r、中心座標を計算します。

array = np.zeros((int(2**11),int(2**11)))
r = int(array.shape[0]/2)
center = (r,r)
p,q= center[0],center[1]

Piの近似値の出力

モンテカルロ法を使用して、試行回数mの時の円内に存在する座標数を計算して、piの近似値を出力します。この時、randintメソッドが閉区間であることに注意します。

def get_pi(m,array):
    n = 0
    for l in range(m):
        i = random.randint(0,array.shape[0]-1)
        j = random.randint(0,array.shape[0]-1)
        array[i,j] = int(1)
        if is_within(i,j,r,p,q):
            n+=int(1)
        else:
            pass 
    return 4*n/m

実行結果

m = 10000の時、3.148という結果が出ました。

円周率の実際の値にかなり近いです。

収束の様子

ここで、試行回数を増やしていった時の収束の様子をmatplotlibを用いて可視化してみます。

具体的には、以下のように試行回数をk回ずつ増やしていき、maxに到達するまでループを回します。

max = max
for m in tqdm(range(1000,max,k)):
    pi = get_pi(m,array)
    plt.scatter(m,pi,s=1)
fig.savefig('pi.png',dpi=700)

まずは、プロット数の最大値を100,k=1の場合の結果を見てみます。

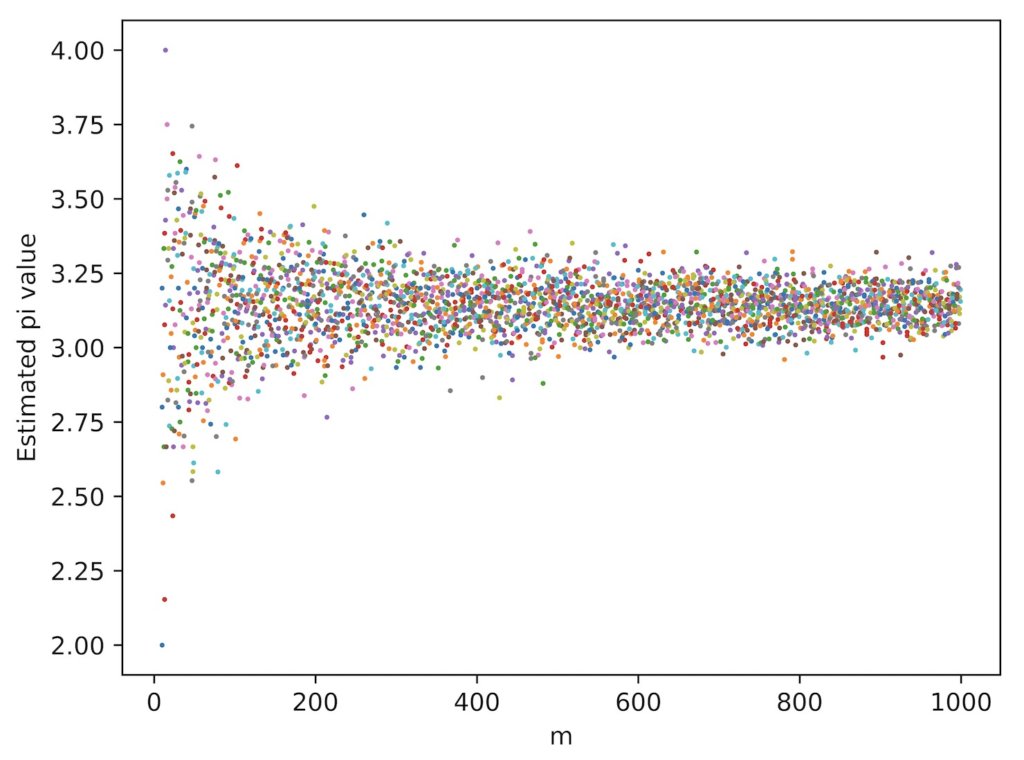
収束に向かっている様子がわかります。

次にプロット数の最大値を1000000,k=1000で実行してみます。

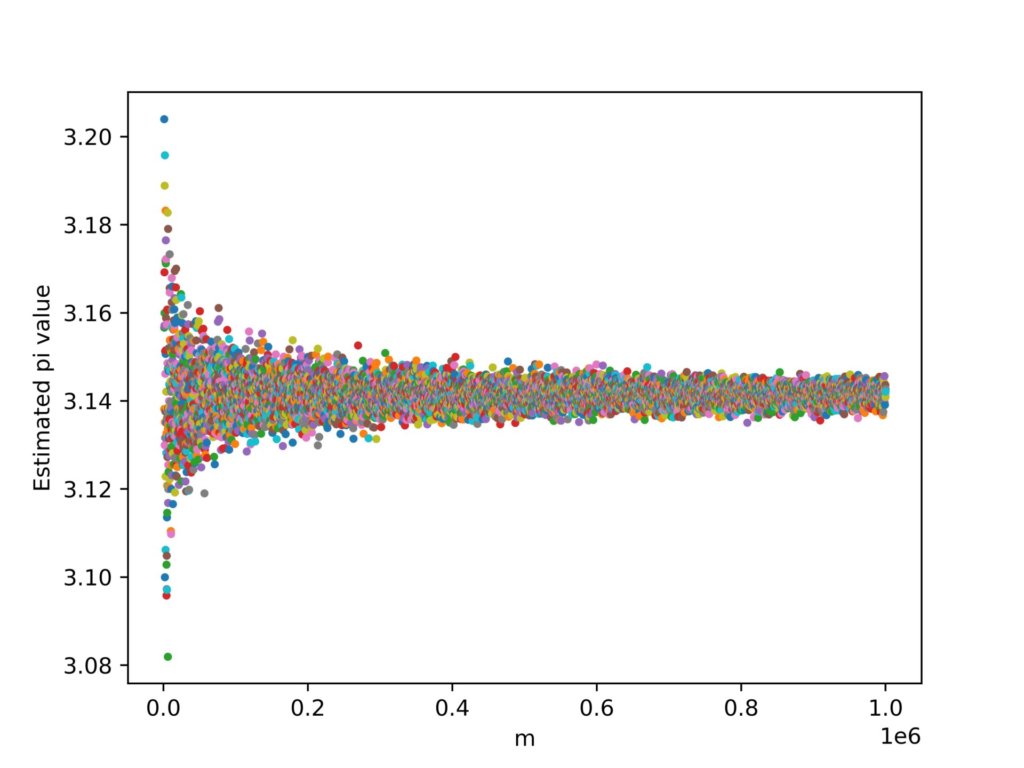
より円周率に近い値に収束していっていることがわかります。

ランダムプロットの様子

ランダムプロットした点（白）を可視化するために、コードを書き換えます。

import numpy as np 
import random
import matplotlib.pyplot as plt 
from tqdm import tqdm 
import cv2 
fig = plt.figure()
def is_within(x,y,radius,p,q):
    if ((x-p)**2 + (y-q)**2)< radius**2:
        return True
def get_pi(m,array):
    n = 0
    for l in range(m):
        i = random.randint(0,array.shape[0]-1)
        j = random.randint(0,array.shape[0]-1)
        array[i,j] = int(255)
        if is_within(i,j,r,p,q):
            n+=int(1)
        else:
            pass 
    return 4*n/m
array = np.zeros((int(2**11),int(2**11)))
r = int(array.shape[0]/2)
center = (r,r)
p,q= center[0],center[1]
plt.xlabel('m')
plt.ylabel('Estimated pi value')
max = 10000
for m in tqdm(range(1000,max,100)):
    pi = get_pi(m,array)
    plt.scatter(m,pi,s=7)
cv2.circle(array, tuple(center), 1, (0, 0, 255), 10)
cv2.circle(array,tuple(center), r, (255, 255, 255), thickness=5, lineType=cv2.LINE_4)
cv2.imwrite('result.png',array)
fig.savefig('pi.png',dpi=700)

以下が出力結果です。一様にランダムな点がプロットされていることがわかります。

ここで一つ疑問に上がったのが、今回は離散的な直交座標上で考えているため、各ピクセルを内外判定していったら面積比が近似できるのではないかということです。

早速以下のように実装してみました。

counter = 0
for i in tqdm(range(array.shape[0])):
    for j in range(array.shape[1]):
        if is_within(i,j,r,p,q):
            counter+= 1 
        else:
            pass 
print(4*counter/array.shape[0]**2)

計算結果は3.1415770649909973となりました。

ピクセルサイズを微小区間まで持っていくことで円周率を絞り込んでいくことができるかもしれません。

モンテカルロ積分【Pythonで学ぶ統計】